题目内容
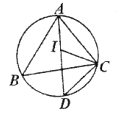
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.

【答案】(1)证明见解析;(2)1
【解析】试题分析:(1)连接OD,根据等边三角形的性质求出∠ODE=90°,根据切线的判定定理证明即可;
(2)连接AD,BF,根据等边三角形的性质求出DC、CF,根据直角三角形的性质求出EC,结合图形计算即可.
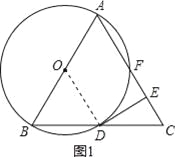
试题解析:(1)如图1,连接OD,∵△ABC是等边三角形,∴∠B=∠C=60°.
∵OB=OD,∴∠ODB=∠B=60°.∵DE⊥AC,∴∠DEC=90°.
∴∠EDC=30°.∴∠ODE=90°.∴DE⊥OD于点D.∵点D在⊙O上,
∴DE是⊙O的切线;
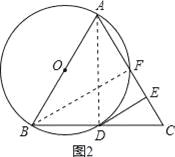
(2)如图2,连接AD,BF,∵AB为⊙O直径,∴∠AFB=∠ADB=90°.∴AF⊥BF,AD⊥BD.
∵△ABC是等边三角形,∴![]() ,
,![]() .
.
∵∠EDC=30°,∴![]() .∴FE=FC﹣EC=1.
.∴FE=FC﹣EC=1.

 直通贵州名校周测月考直通名校系列答案
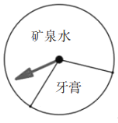
直通贵州名校周测月考直通名校系列答案【题目】如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物50元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在某一区域就可以获得该区域相对应的奖品.若恰巧落在两区域交界线上,则重新转动转盘.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“矿泉水”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
假如你去转动该转盘一次,你获得牙膏的概率约是______.(用小数表示,结果保留一位小数)
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … | -2 | -1 | 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中正确的是______.(填写序号)
①抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ; ②函数
; ②函数![]() 的最大值为6;
的最大值为6;
③抛物线的对称轴是直线![]() ; ④在对称轴左侧,
; ④在对称轴左侧,![]() 随
随![]() 增大而增大.
增大而增大.