题目内容
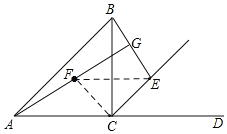
【题目】如图在△ABC中,∠ACB=90°,AC=BC,E为外角∠BCD平分线上一动点(不与点C重合),点E关于直线BC的对称点为F,连接BE,连接AF并延长交直线BE于点G.
(1)求证:AF=BE;
(2)用等式表示线段FG,EG与CE的数量关系,并证明.
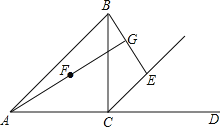
【答案】(1)证明见解析;(2)GE2+GF2=2CE2.证明见解析.
【解析】
(1)根据边角证明△FCA≌△ECB,所以AF=BE;
(2)FG,EG与CE的数量关系:GE2+GF2=2CE2,先证明∠EGF=∠ECF=90°,然后利用勾股定理证明即可.
解:(1)如图,连接CF.
∵,∠ACB=90°,CE平分∠BCD,
∴∠BCE=45°,
∵点E、F关于直线BC对称,
∴CE=CF,
∠FCB=∠BCE=45°,
∴∠FCA=45°,
在△FCA与△ECB中,
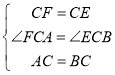
∴△FCA≌△ECB(SAS),
∴AF=BE;
(2)FG,EG与CE的数量关系:GE2+GF2=2CE2,
证明:∵△FCA≌△ECB,
∴∠AFC=∠BEC,
∵∠AFC+∠CFG=180°,
∴∠CFG+∠CEG=180°,
∴∠ECF+∠EGF=180°,
∵∠ECF=45°+45°=90°,
∴∠EGF=90°,
连接EF,
∴GE2+GF2=EF2,
∵CE=CF,
∴CE2+CF2=2CE2=EF2,
∴GE2+GF2=2CE2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目