��Ŀ����
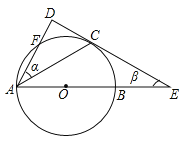
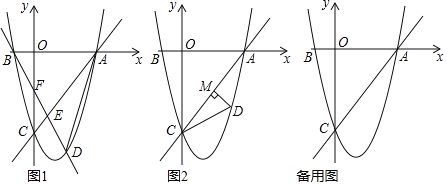
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y��![]() x��4��������y��
x��4��������y��![]() +bx+c����������������A��C����������x����һ����Ϊ��B��
+bx+c����������������A��C����������x����һ����Ϊ��B��
��1���������߽���ʽ��
��2��������D��ֱ��AC�·����������ϣ�
����ֱ��BD�����߶�AC�ڵ�E����y���ڵ�F������AD�����ADE���CEF���������ֵ������ʱ��D�����ꣻ
����ͼ2����DM��ֱ��AC������Ϊ��M���Ƿ���ڵ�D��ʹ��CDM��ij����ǡ���ǡ�ACO��һ�룿�����ڣ�ֱ��д����D�ĺ����ꣻ�������ڣ�˵�����ɣ�
���𰸡���1��y��![]() ��
��
��2������m��![]() ʱ��S��ADE��S��CEF�����ֵΪ
ʱ��S��ADE��S��CEF�����ֵΪ![]() ����ʱ��D����Ϊ��
����ʱ��D����Ϊ��![]() ��
��![]() ����
����
�����ڣ���D�ĺ�����Ϊ��D������Ϊ![]() ��
��![]() ��
��
��������
��1�������C��0����4��A��3��0����Ȼ�����y��![]() +bx+c���Ӷ���������߽���ʽ��
+bx+c���Ӷ���������߽���ʽ��
��2������D��m��![]() ������tan��ABD��
������tan��ABD��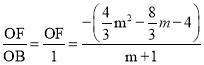 ��Ȼ����m�Ĵ���ʽ��ʾ��ADE����CEF�������ö��κ�����ֵ������ֵ��
��Ȼ����m�Ĵ���ʽ��ʾ��ADE����CEF�������ö��κ�����ֵ������ֵ��
������ACO��ƽ����CP��x���ڵ�P����P��PH��AC�ڵ�H�����tan��PCH��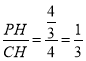 ��Ȼ�������������ۣ�����MCD��
��Ȼ�������������ۣ�����MCD��![]() ��ACO����PCHʱ������MDC��
��ACO����PCHʱ������MDC��![]() ��ACO����PCHʱ��
��ACO����PCHʱ��
��1������y��![]() x��4����x��0����y����4����C��0����4����
x��4����x��0����y����4����C��0����4����
��y��0����x��3��
��A��3��0����
�ѵ�A��C������������߽���ʽ��
�ã�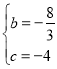 ���
���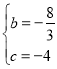 ��
��
�������߽���ʽΪy��![]() ��
��
��2����D��m��![]() ����0��m��3
����0��m��3
������OD����ΪB����1��0����D��m��![]() ��
��
tan��ABD��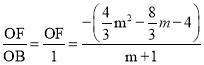 ��
��
��OF����![]() ��m��3����
��m��3����
��OA��3��OC��4��
��S��ADE��S��CEF��S�ı���AOFD��S��AOC��![]() AO|yD|+
AO|yD|+![]() OF|xD|��
OF|xD|��![]() OAOC
OAOC
��![]() [3����
[3����![]() m2+
m2+![]() m+4����
m+4����![]() ��m��3��m��3��4]
��m��3��m��3��4]
����![]() m2+6m
m2+6m
����![]() ��m��
��m��![]() ��2+
��2+![]() ��
��
���Ե�m��![]() ʱ��S��ADE��S��CEF�����ֵΪ
ʱ��S��ADE��S��CEF�����ֵΪ![]() ����ʱ��D����Ϊ
����ʱ��D����Ϊ![]() ��
��
�ڴ��ڣ���D�ĺ�����Ϊ��D������Ϊ![]() ��
��![]() ��
��
����ACO��ƽ����CP��x���ڵ�P����P��PH��AC�ڵ�H��
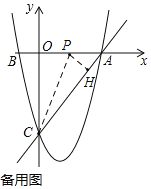
��CH��CO��4��OP��PH��
��OP��PH��x����PA��3��x��
��OC��4��OA��3��
��AC��5��AH��1��
��Rt��PHA��
PH2+AH2��AP2��
��/span>x2+12����3��x��2��
���x��![]() ��
��
��tan��PCH��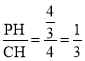 ��
��
����D��DG��x���ڵ�G������M��ME��x�ᣬ��y�ύ�ڵ�E����DG���ڵ�F��
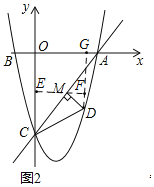
��M��m��![]() ������ME��m��FG��OE��
������ME��m��FG��OE��![]() ��CE��
��CE��![]() ��
��
��DM��ֱ��AC��
���CEM�ס�MFD��
��![]() ��
��
����MCD��![]() ��ACO����PCHʱ��
��ACO����PCHʱ��
tan��MCD��tan��PCH��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��MF��![]() CE��
CE��![]() ��DF��
��DF��![]() ME��
ME��![]() ��
��
��EF��EM+MF��m+![]() ��
��![]() ��DG��DF+FG��
��DG��DF+FG��![]() m+��
m+��![]() ������m+4��
������m+4��
��D��![]() ��m��4����
��m��4����
����D�������y��![]() ��
��
m��4��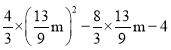 ��
��
���m��0����ȥ����m��![]()
����MDC��![]() ��ACO����PCHʱ��
��ACO����PCHʱ��
tan��MDC��tan��PCH��![]() ��
��
��![]() ��
��
��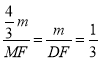 ��
��
MF��4m��DF��3m��
��EF��EM+MF��m+4m��5m��
DG��DF+FG��3m��![]() ��
��
��D��5m�� ![]() ����
����
����D�������y��![]() ��
��
![]() ��
��
���x��0����ȥ����x��![]() ��
��
���ϣ���D������Ϊ![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
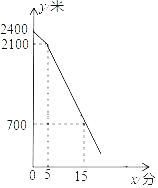
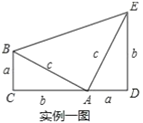
�Ķ��쳵ϵ�д�����Ŀ��ij�о���ƶ�����Ѿ����빥��Σ�ƶ�����Ŵ�ү��ij��λ�İ���£���һƬ�µظ������ֲ�˴�ӣ��.������ʽ�������ۣ�������30���У���һ������20ǧ�ˣ�Ϊ��������������һ��ʱ���ڲ�ȡ���۴�ʩ��ÿ���ǰһ�������4ǧ�ˣ����ۼ۲���ʱ��������Ҳ�������仯����֪��ֲ���۴�ӣ�ҵijɱ�Ϊ18Ԫ��ǧ�ˣ����![]() ������ۼ�
������ۼ�![]() Ԫ��ǧ�ˣ�
Ԫ��ǧ�ˣ�![]() ��
��![]() ������ϵ���±���
������ϵ���±���
��һ
���� | 1 | 2 | 3 | ���� | ���� | 20 |
�ۼۣ�Ԫ��ǧ�ˣ� | 37.5 | 37 | 36.5 | ���� | ���� | 28 |
����
���� | 21 | 22 | ���� | ���� | 30 |
�ۼۣ�Ԫ��ǧ�ˣ� | 28 | 28 | ���� | ���� | 28 |
��1����![]() ��
��![]() ��������ʽ��
��������ʽ��
��2�������۴�ӣ�ҵڼ���ʱ����������������������Ƕ��٣�
��3�����۴�ӣ�ҵ�30���У�����������
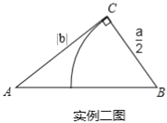
����Ŀ���ס�������ͬѧ�ֱ����6�����ѵ����ѵ���ɼ�����λ���������±�
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 9 | 8 | 6 | 7 | 8 | 10 |
�� | 8 | 7 | 9 | 7 | 8 | 8 |
�����ǵ�ѵ���ɼ������·���������˵����ȷ���ǣ�������
A. ����ѵ���ɼ���ƽ������ͬ B. ����ѵ���ɼ�����λ����ͬ
C. ����ѵ���ɼ���������ͬ D. ����ѵ���ɼ��ķ��ͬ