题目内容
【题目】在Rt△ABC中,∠C=90°.
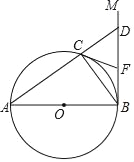
(1)如图①,点O在斜边AB上,以点O为圆心,OB长为半径的圆交AB于点D,交BC于点E,与边AC相切于点F.求证:∠1=∠2;
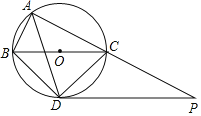
(2)在图②中作⊙M,使它满足以下条件:①圆心在边AB上;②经过点B;③与边AC相切.(尺规作图,只保留作图痕迹,不要求写出作法)
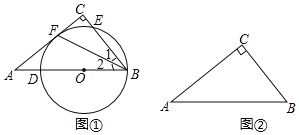
【答案】(1)证明见解析;(2)作图见解析.
【解析】
(1)连接OF,可证得OF∥BC,结合平行线的性质和圆的特性可求得∠1=∠OFB=∠2,可得出结论;
(2)由(1)可知切点是∠ABC的角平分线和AC的交点,圆心在BF的垂直平分线上,由此即可作出⊙M.
解:(1)证明:如图①,连接OF,
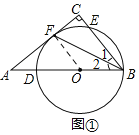
∵AC是⊙O的切线,
∴OE⊥AC,
∵∠C=90°,
∴OE∥BC,
∴∠1=∠OFB,
∵OF=OB,
∴∠OFB=∠2,
∴∠1=∠2.
(2)如图②所示⊙M为所求.①
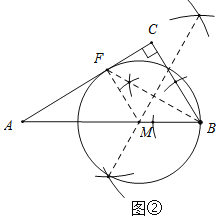
①作∠ABC平分线交AC于F点,
②作BF的垂直平分线交AB于M,以MB为半径作圆,
即⊙M为所求.
证明:∵M在BF的垂直平分线上,
∴MF=MB,
∴∠MBF=∠MFB,
又∵BF平分∠ABC,
∴∠MBF=∠CBF,
∴∠CBF=∠MFB,
∴MF∥BC,
∵∠C=90°,
∴FM⊥AC,
∴⊙M与边AC相切.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目