如图.在梯形ABCD中.AD∥BC.AD=2.BC=4.点M是AD的中点.△MBC是等边三角形．动点P.Q分别在线段BC和MC上运动.且∠MPQ=60°保持不变．以下四个结论:①梯形ABCD是等腰梯形,②△BMP∽△CPQ,③△MPQ是等边三角形,④设PC=x.MQ=y.则y关于x的函数解析式是二次函数．(1)判断其中正确的结论是哪几个?(2)从你认为是正确的结论中选一� 题目和参考答案——青夏教育精英家教网—

题目内容

如图，在梯形ABCD中，AD∥BC，AD=2，BC=4，点M是AD的中点，△MBC是等边三角形．动点P、Q分别在线段BC和MC上运动（不与端点重合），且∠MPQ=60°保持不变．以下四个结论：①梯形ABCD是等腰梯形；②△BMP∽△CPQ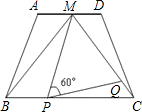

；③△MPQ是等边三角形；④设PC=x，MQ=y，则y关于x的函数解析式是二次函数．
（1）判断其中正确的结论是哪几个？
（2）从你认为是正确的结论中选一个加以证明．

分析：（1）①首先由等边三角形的性质，易证：△AMB≌△DMC，则可证得AB=CD，即得四边形ABCD是等腰梯形；
②利用有两角对应相等的三角形相似，即可证得：△BMP∽△CPQ；
③由MP不一定等于PQ，即可知：△MPQ不一定是等边三角形；
④由相似三角形的对应边成比例即可求得y与x的关系．
（2）根据（1）中的分析，选择①②④中的任一个证明即可．

解答：解：（1）①∵△MBC是等边三角形，
∴MB=MC，∠MBC=∠MCB=60°，
∵AD∥BC，
∴∠AMB=∠MBC，∠DMC=∠MCB，
∴∠AMB=∠DMC，
∵AM=DM，
∴△AMB≌△DMC，
∴AB=CD，
∴梯形ABCD是等腰梯形．故①正确；
②∵∠1+∠MPB=120°，∠2+∠MPB=180°-∠MPQ=120°，
∴∠1=∠2，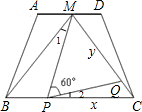

∵∠MBP=∠MPQ=60°，
∴△BMP∽△CPQ．故②正确；
③∵MP不一定等于PQ，
∴△MPQ不一定是等边三角形．故③错误；
④∵△BMP∽△CPQ，
∴

，
∵BC=4，
∴MB=MC=4，
∵PC=x，MQ=y，则BP=4-x，CQ=4-y，
∴

4-x

4-y

，
∴y=

x²-x+4，故④正确．
∴正确的是①②④；
（2）选①的证明：
思路：证明△ABM≌△DCM（SAS）；
∴AB=DC，
∴ABCD是等腰梯形；
选②的证明：∠MBP=∠PCQ=60°，∠1+60°=∠2+60°（外角），
∴∠1=∠2，
∴△BMP∽△CPQ；
选④的证明：先证明相似，过程同②：△BMP∽△CPQ，
∴

，
即

4-y

4-x

，
∴y=

x²-x+4．

点评：此题考查了梯形的性质，全等三角形的判定与性质，相似三角形的判定与性质以及等边三角形的性质等知识．此题综合性很强，题目难度较大，注意数形结合思想的应用．