题目内容
【题目】如图,在平面直角坐标系中,点A(4,2),点B在第一象限,AB平行于x轴且AB=5.
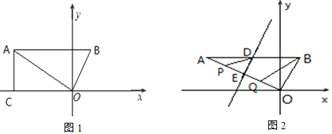
(1)点B的坐标为_______.
(2)如图1,过点A作AC⊥x轴于C,在x轴上是否存在点D,使得△AOC与△BOD相似?
(3)如图2,将△AOB折叠,使得点A刚好落在O处,此时折痕交AB于点D,交AO于点E,在直线AO上有两个动点P,Q(点P在点Q的左侧),且线段PQ=![]() ,求四边形BDPQ的周长最小值.
,求四边形BDPQ的周长最小值.
【答案】(1)(1,2);(2)存在,D(1,0)或(5,0);(3)周长最小值为![]()
【解析】
(1)由AB//x轴可得点B纵坐标,根据AB=5可求出得B横坐标,即可得到答案;(2)根据A、B两点坐标可求出OA、OB的长,根据勾股定理逆定理可得△AOB是直角三角形,∠AOB=90°,当点D在x轴负半轴时,∠BOD>90°,不能与Rt△AOC相似;当点D在x轴正半轴时,根据同角的余角相等可得∠CAO=∠DOB,分别讨论∠OBD=90°和∠ODB=90°两种情况,求出点D坐标即可;(3)由折叠性质可得DE⊥OA,OE=![]() OA=
OA=![]() ,由OB⊥OA可得DE//BO,DE和OB是DP和BQ的最小值,由点E是OA中点DE是△AOB的中位线,可得BD=
,由OB⊥OA可得DE//BO,DE和OB是DP和BQ的最小值,由点E是OA中点DE是△AOB的中位线,可得BD=![]() AB,DE=
AB,DE=![]() OB,进而求出四边形DEOB的周长即可得答案.
OB,进而求出四边形DEOB的周长即可得答案.
(1)∵AB//x轴,A(-4,2),
∴点B的纵坐标为2,
∵AB=5,
∴点B的横坐标为-4+5=1,
∴点B坐标为(1,2).
故答案为:(1,2)
(2)∵A(-4,2),B(1,2),
∴OA=2![]() ,OB=
,OB=![]() ,
,
∵AB2=25,OA2=20,OB2=5,
∴AB2=OA2+OB2,
∴△OAB是直角三角形,∠AOB=90°,
当点D在x轴负半轴时,∠BOD>90°,不能与Rt△AOC相似;
当点D在x轴正半轴时,
∵∠AOC+∠BOD=90°,∠AOC+∠CAO=90°,
∴∠CAO=∠DOB,
如图,当∠OBD2=90°时,
∵∠D2OB=∠CAO,∠OBD2=∠ACO=90°,
∴△OBD2∽△ACO,
∴![]() ,即
,即![]() ,
,
∴OD2=5,
∴D2(5,0).
当∠OD1B=90°时,
∵∠BOD1=∠CAO,∠OD1B=∠ACO=90°,
∴△BOD1∽△OAC,
∵∠OD1B=90°,B(1,2)
∴OD1=1,
∴D1(1,0)

综上所述:存在点D,使得△AOC与△BOD相似,点D坐标为(1,0)或(5,0).
(3)∵将△AOB折叠,使得点A刚好落在O处,此时折痕交AB于点D,交AO于点E,
∴DE⊥OA,AE=OE=![]() OA=
OA=![]()
∵∠AOB=90°,
∴DE//OB,
∴AD=BD=![]() AB=
AB=![]() ,
,
∴DE是△AOB的中位线,
∴DE=![]() OB=
OB=![]() ,
,
∵DE⊥OA,OB⊥OA,OE=![]() ,
,
∴DE和BO即是DP和BQ的最小值,
∴四边形BDPQ的周长最小值为BD+DE+OE+OB=![]() +
+![]() +
+![]() +
+![]() =
=![]() .
.