Question

【题目】如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，若AC=FC．

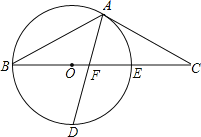
（1）求证：AC是⊙O的切线：

（2）若BF=8，DF=，求⊙O的半径r．

Answer 1

【答案】解：（1）证明：连接OA、OD，

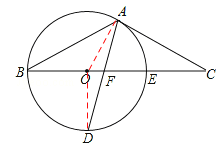
∵D为弧BE的中点，∴OD⊥BC。

∴∠DOF=90°。∴∠D+∠OFD=90°。

∵AC=FC，OA=OD，

∴∠CAF=∠CFA，∠OAD=∠D。

∵∠CFA=∠OFD，∴∠OAD+∠CAF=90°。

∴OA⊥AC。

∵OA为半径，∴AC是⊙O切线。

（2）当F在半径OE上时，∵⊙O半径是r，∴OD=r，OF=8﹣r。

在Rt△DOF中，r2+（8﹣r）2=（）2，解得r=或r=（舍去）；

当F在半径OB上时，∵⊙O半径是r，∴OD=r，OF=r﹣8。

在Rt△DOF中，r2+（r﹣8）2=（）2，解得r=或r=（舍去）。

∴⊙O的半径r为。