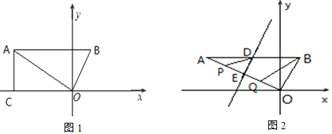题目内容
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G。
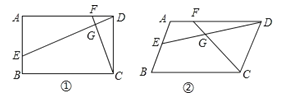
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且AD·DF=AE·DC,求证:DE⊥CF;
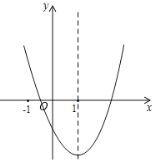
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DE·CD=CF·DA.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据已知条件得到四边形ABCD是矩形,由矩形的性质得到∠A=∠FDC=90°,根据相似三角形的性质得到∠CFD=∠AED,根据余角的性质即可得到结论;
(2)根据已知条件得到△DFG∽△DEA,推出![]() ,根据△CGD∽△CDF,得到
,根据△CGD∽△CDF,得到![]() ,等量代换即可得到结论;
,等量代换即可得到结论;
(1)证明:∵AB∥CD,AB=CD,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵ADDF=AEDC,
∴![]() ,
,
∴△AED∽△DFC,
∴∠CFD=∠AED,
∵∠ADE+∠AED=90°,
∴∠ADE+∠CFD=90°,
∴∠DGF=90°,
∴DE⊥CF;
(2)证明:∵∠A=∠EGC,∠ADE=∠GDF,
∴△DFG∽△DEA,
∴![]() =
=![]() ,
,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,∠AED=∠EDC,
∴∠B=∠ADC,
∵△DFG∽△DEA,
∴∠AED=∠DFG,
∴∠DFC=∠GDC,
∵∠DCG=∠FCD,
∴△CGD∽△CDF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴DECD=CFDA;

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目