题目内容
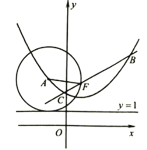
【题目】已知抛物线y=![]() x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
x2+bx+c经过点A(﹣2,0)、B(0、﹣4)与x轴交于另一点C,连接BC.
(1)求抛物线的解析式.
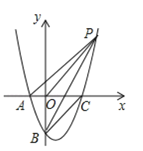
(2)如图,P是第一象限内抛物线上一点,且![]() ,求P点坐标.
,求P点坐标.
(3)在抛物线上是否存在点D,直线BD交x轴于点E,使![]() ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
ABE与以A,B,C,E中的三点为顶点的三角形相似(不重合)?若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2﹣x﹣4;(2)P (6,8);(3)存在,D (8,20)或
x2﹣x﹣4;(2)P (6,8);(3)存在,D (8,20)或![]()
【解析】
(1)利用待定系数法求抛物线的解析式;
(2)令y=0求抛物线与x轴的交点C的坐标,作△POB和△PBC的高线,根据面积相等可得OG=CF,证明△OEG≌△CEF,得OE=CE,即得到点E的坐标为(2,0),利用待定系数法求得直线PB的解析式,解方程组即可求得P点坐标;
(3)先利用概率的知识分析A,B,C,E中的三点为顶点的三角形,有两个三角形与△ABE有可能相似,即△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,根据存在公共角∠BAE=∠BAC,可得△ABE∽△ACB,列比例式可得E的坐标,利用待定系数法求直线BE的解析式,与抛物线列方程组可得交点D的坐标;
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,同理可得结论.
(1)把点A(-2,0),B(0、-4)代入抛物线![]() 得:
得:
![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(2)当![]() 时,
时,![]() ,
,
解得:![]() 或4,
或4,
∴点C的坐标为(4,0),
如图1,过O作OG⊥BP于G,过C作CF⊥BP于F,PB交![]() 轴于点E,
轴于点E,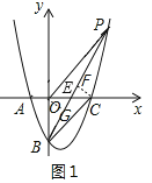
∵S△PBO=S△PBC,
∴![]() BPOG=
BPOG=![]() BPCF,
BPCF,
∴OG=CF,
∵∠OEG=∠CEF,∠OGE∠CFE,
∴△OEG≌△CEF(AAS),
∴OE=CE,
点E的坐标为(2,0),
设直线PB的解析式为![]() ,
,
把点E(2,0)代入得,![]()
解得:![]() ,
,
∴直线PB的解析式为![]() ,
,
解方程组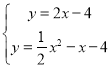 得:
得: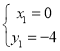 (舍去)或
(舍去)或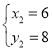 ,
,
∴点P的坐标为(6,8);
(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,
∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,
(3)以A,B,C,E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE,四种,其中△ABE重合,不符合条件,△ACE不能构成三角形,
∴当△ABE与以A,B,C,E中的三点为顶点的三角形相似,存在两个三角形:△ABC和△BCE,
①当△ABE与以A,B,C中的三点为顶点的三角形相似,如图2,
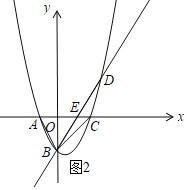
由(1)得:点A(-2,0),B(0,-4),C(4,0),
∴OB=OC=4,
![]() ,
,
![]() ,
,
∴∠OBC=∠OCB=45°,
∵∠BAE=∠BAC,∠ABE≠∠ABC,
∴∠ABE=∠ACB=45°,
∴△ABE∽△ACB,
∴![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
点![]() 的坐标为(
的坐标为(![]() ,0);
,0);
设直线BE的解析式为![]() ,
,
把点E(![]() ,0)代入得,
,0)代入得,![]() ,
,
∴直线BE的解析式为![]() ,
,
解方程组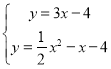 得:
得: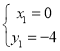 (舍去)或
(舍去)或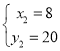 ,
,
∴点D的坐标为(8,20);
②当△ABE与以B,C、E中的三点为顶点的三角形相似,如图3,此时E在C的左边,
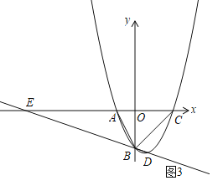
∵∠BEA=∠BEC,
∴当∠ABE=∠BCE时,△ABE∽△BCE,
∴![]() ,
,
设![]() ,
,![]() ,
,
Rt△BOE中,由勾股定理得:![]() ,
,
∴![]() ,
,
即![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 或
或![]() ,
,
∵![]() ,∠AEB或∠BEC是钝角,如图4,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
,∠AEB或∠BEC是钝角,如图4,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
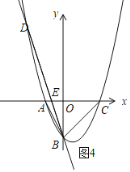
∴E(-12,0);
同理得BE的解析式为:![]() ,
,
解方程组 得:
得: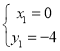 (舍去)或
(舍去)或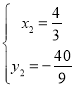 ,
,
∴点D的坐标为(![]() ,
,![]() );
);
同理可得E在C的右边时,△ABE∽△BCE,
∴![]() ,
,
设![]() ,
,![]() ,
,
Rt△BOE中,由勾股定理得:![]() ,
,
∴![]() ,
,
即![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() (舍去)或
(舍去)或![]() ,
,
∵![]() ,∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
,∠BEC是钝角,此时△ABE与以B,C、E中的三点为顶点的三角形不相似,
综上,点D的坐标为(8,20)或(![]() ,
,![]() ).
).

 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案【题目】合理饮食对学生的身体、智力发育和健康起到了极其重要的作用,只有荤食和素食的合理搭配,才能强化初中生的身体素质,某校为了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
收集数据:
从七、八年级两个年级中各抽取![]() 名学生,进行了体质健康测试,测试成绩(百分制)如下:
名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:![]()
八年级:![]()
整理数据:
年级 |
|
|
|
|
七年级 |
|
|
|
|
八年级 |
|
|
|
|
(说明:![]() 为优秀,
为优秀,![]() 为良好,
为良好,![]() 为及格,
为及格,![]() 为不及格)
为不及格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ,
,
(2)比较这两组样本数据的平均数、中位数和众数,你认为哪个年级的体质健康成绩比较好?请说明理由
(3)若七年级共有![]() 名学生,请估计七年级体质健康成绩优秀的学生人数
名学生,请估计七年级体质健康成绩优秀的学生人数