题目内容
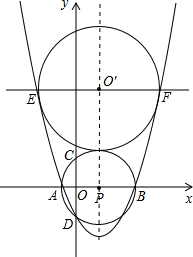
已知⊙P的圆心坐标为(1.5,0),半径为2.5,⊙P与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点D.
(1)求D点的坐标;
(2)求过A、B、D三点的抛物线的解析式;
(3)设平行于x轴的直线交此抛物线于E、F两点,问:是否存在以线段EF为直径的圆O'恰好与⊙P相外切?若存在,求出其半径r及圆心O'的坐标;若不存在,请说明理由.

(1)求D点的坐标;
(2)求过A、B、D三点的抛物线的解析式;
(3)设平行于x轴的直线交此抛物线于E、F两点,问:是否存在以线段EF为直径的圆O'恰好与⊙P相外切?若存在,求出其半径r及圆心O'的坐标;若不存在,请说明理由.

(1)由已知,得OA=1,OB=4,
∴OD2=OA•OB=1×4,OD=2
∴D点的坐标为(0,-2);
(2)设过A、B、D三点多抛物线解析式为y=ax2+bx+c,把A(-1,0)、B(0,-2)的坐标代入解析式,得:
∴
∴过点A、B、D三点多抛物线的解析式为y=
x2-
x-2;
(3)存在.配方y=
x2-
x-2=
(x-
)2-
抛物线的对称轴为x=
,圆心O’应在对称轴上.分两种情况:
①当以线段EF为直径的圆O′在x轴上方时,F(
+r,
+r)在抛物线y=
x2-
x-2上,
∴
+r=
(
+r)2-
(
+r)-2,
整理得4r2-8r-45=0,
解得r=
或r=-
(舍去)
∴半径r=
.圆心O′(
,7);
②当以线段EF为直径的圆O′在x轴下方时:F(
+r,-
-r)在抛物线y=
x2-
x-2上,
∴-
-r=
(
+r)2-
(
+r)-2,
整理得4r2+8r-5=0,
解得r=
或r=-
(舍去)
∴半径r=
,圆心O′(
,-3).
∴OD2=OA•OB=1×4,OD=2
∴D点的坐标为(0,-2);
(2)设过A、B、D三点多抛物线解析式为y=ax2+bx+c,把A(-1,0)、B(0,-2)的坐标代入解析式,得:
|
∴
|
∴过点A、B、D三点多抛物线的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
(3)存在.配方y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 25 |
| 8 |
抛物线的对称轴为x=
| 3 |
| 2 |
①当以线段EF为直径的圆O′在x轴上方时,F(
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
整理得4r2-8r-45=0,
解得r=
| 9 |
| 2 |
| 5 |
| 2 |
∴半径r=
| 9 |
| 2 |
| 3 |
| 2 |
②当以线段EF为直径的圆O′在x轴下方时:F(
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴-
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
整理得4r2+8r-5=0,
解得r=
| 1 |
| 2 |
| 5 |
| 2 |
∴半径r=
| 1 |
| 2 |
| 3 |
| 2 |


练习册系列答案
相关题目


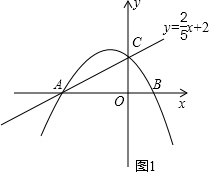
 ,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.
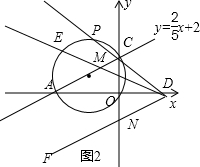


 的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.
的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.