题目内容
【题目】已知一次函数![]() 的图象分别交x轴、y轴于A、B两点,且与反比例函数
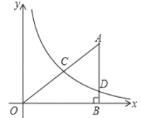
的图象分别交x轴、y轴于A、B两点,且与反比例函数![]() 的图象在第一象限交于点C(4,n),CD⊥x轴于D.
的图象在第一象限交于点C(4,n),CD⊥x轴于D.
(1)求m、n的值,并在给定的直角坐标系中作出一次函数的图象;

(2)如果点P、Q分别从A、C两点同时出发,以相同的速度沿线段AD、CA向D、A运动,设AP=k.
①k为何值时,以A、P、Q为顶点的三角形与△AOB相似?
②k为何值时,△APQ的面积取得最大值并求出这个最大值.
【答案】(1)m=3,n=6,图像见解析;(2)见解析
【解析】
试题(1)首先根据反比例函数的解析式求得n的值,再根据点C的坐标求得m的值.根据直线与坐标轴的交点坐标准确画出函数的图象;
(2)①已知△AOB是直角三角形,要使以A、P、Q为顶点的三角形与△AOB相似,则∠APQ=90°或∠AQP=90°.根据题意表示对应的两条边,再根据相似三角形的对应边的比相等列方程求解;②首先根据相似三角形的对应边的比相等表示出AP边上的高,再进一步表示三角形的面积,根据函数解析式分析其最值.
解:(1)把(4,n)代入反比例函数![]() ,得:n=6
,得:n=6
把(4,6)代入一次函数y=![]() x+m,得:m=3
x+m,得:m=3
∴y=![]() x+3.
x+3.
令x=0,则y=3;令y=0,则x=﹣4.(如图)
(2)①根据题意,得AP=CQ=k,根据勾股定理,得AC=10,则AQ=10﹣k
当∠APQ=90°时,则有![]() ,即
,即![]() ,k=
,k=![]() ;
;
当∠AQP=90°时,则有![]() ,即
,即![]() ,k=
,k=![]() .
.
②作QM⊥x轴于M,则△AQM∽△ACD,
则有![]() ,即
,即![]() ,QM=
,QM=![]() .
.
则S△APQ=![]() ×
×![]() ×k=﹣
×k=﹣![]() k2+3k
k2+3k
所以当k=5时,则该三角形的面积的最大值是7.5.



练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目