题目内容
【题目】在平面直角坐标系内,已知![]() .
.
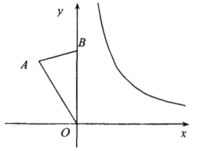
(1)点A的坐标为(____,______);
(2)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() .
.
①当![]() 时,点
时,点![]() 恰好落在反比例函数
恰好落在反比例函数![]()
![]() 的图象上,求
的图象上,求![]() 的值;
的值;
②在旋转过程中,点![]() 能否同时落在上述反比例函数的图象上,若能,求出
能否同时落在上述反比例函数的图象上,若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】(1)A(-1,![]() );(2)①
);(2)①![]() ;②
;②![]() ,理由见解析
,理由见解析
【解析】
(1)作AC⊥x轴于点C,在直角△AOC中,利用三角函数即可求得AC、OC的长度,则A的坐标即可求解;
(2)①当a=30时,点B的位置与A一定关于y轴对称,在B的坐标可以求得,利用待定系数法即可求得反比例函数的解析式;
②当![]() =60°时,旋转后点的横纵坐标正好互换,则一定都在反比例函数的图象上.
=60°时,旋转后点的横纵坐标正好互换,则一定都在反比例函数的图象上.
解:(1)作AC⊥x轴于点C,
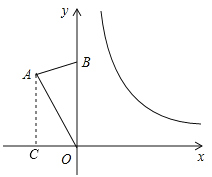
在直角△AOC中,∠AOC=90°-∠AOB=60°,
则AC=OAsin∠AOC=2×![]() =
=![]() ,OC=OAcos60°=2×
,OC=OAcos60°=2×![]() =1,
=1,
则A的坐标是(-1,![]() );
);
(2)①当![]() =30°时,B的坐标与A(-1,
=30°时,B的坐标与A(-1,![]() )一定关于y轴对称,
)一定关于y轴对称,
则旋转后的点B(1,![]() ).
).
把(1,![]() )代入函数解析式得:k=
)代入函数解析式得:k=![]() ;
;
②当![]() =60°时,旋转后点A(1,
=60°时,旋转后点A(1,![]() ),点B(
),点B(![]() ,1),
,1),
∵xy=![]() ,
,
∴当![]() =60°,A、B能同时落在上述反比例函数的图象上.
=60°,A、B能同时落在上述反比例函数的图象上.

 名校课堂系列答案
名校课堂系列答案【题目】问题背景:
学校广播站要招聘一名播音员,需考查应聘学生的应变能力、知识面、朗读水平三个项目,决赛中,小文和小明两位同学的各项成绩如下表,评委计算三项测试的平均成绩,发现小明与小文的相同.
测试项目 | 测试成绩 | |
小文 | 小明 | |
应变能力 | 70 | 80 |
知识面 | 80 | 72 |
朗诵水平 | 87 | 85 |
(1)评委按应变能力占10%,知识面占40%,朗诵水平占50%计算加权平均数,作为最后评定的总成绩,成绩高者将被录用,小文和小明谁将被录用?
(2)若(1)中应变能力占![]() ,知识面占
,知识面占![]() ,其中
,其中![]() ,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的
,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的![]() 的值.
的值.