题目内容
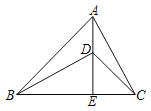
【题目】如图,四边形ABCD,AD∥BC,AD=2![]() ,BD=BC=3
,BD=BC=3![]() ,AC=4
,AC=4![]() ,将AC沿着AD方向平移至DE,使得点A与点D对应,点C与点E对应.
,将AC沿着AD方向平移至DE,使得点A与点D对应,点C与点E对应.
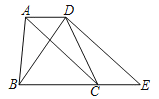
(1)猜想DE与BD的位置关系,并证明你的结论;
(2)求四边形ABCD的面积.
【答案】(1)DE⊥BD,理由见解析;(2)四边形ABCD的面积为12.
【解析】
(1)根据平移的性质和勾股定理的逆定理解答即可;
(2)根据三角形面积公式和梯形的面积公式解答即可.
(1)DE⊥BD,理由如下:
由平移可得:AD=CE=2![]() ,AC=DE=4
,AC=DE=4![]() ,
,
在△BDE中,DE=4![]() ,BE=BC+CE=5
,BE=BC+CE=5![]() ,BD=3
,BD=3![]() ,
,
∴BE2=BD2+DE2,
∴△BDE是直角三角形,
∴BD⊥DE;
(2)过D作DF⊥BE,
在Rt△BDE中,
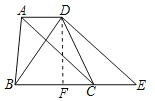
DF=![]() ,
,
∴四边形ABCD的面积=![]() =12
=12

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目