题目内容
【题目】在直角坐标平面xOy中,二次函数y=x2+2(m+2)x+m﹣2图象与y轴交于(0,﹣3)点.
(1)求该二次函数的解析式,并画出示意图;
(2)将该二次函数图象向左平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
【答案】(1)y=x2+2x﹣3;如图见解析;
(2)二次函数图象向左平移1个单位后经过坐标原点,平移后所得图象与x轴的另一个交点坐标为(﹣4,0).
【解析】
(1)把点(0,-3)代入二次函数y=x2+2(m+2)x+m-2中得到m-2=-3,求出m=-1,即可确定抛物线的解析式;把y=x2+2x-3配成顶点式为y=(x+1)2-4,此抛物线的对称轴为直线x=-1,顶点坐标为(-1,-4),由此可画出抛物线的示意图;
(2)先令y=0,即x2+2x-3=0,解方程确定二次函数图象与x轴的两个交点坐标分别为(-3,0)、(1,0),要把点(1,0)向左平移到原点,需移一个单位,则点(-3,0)要移到点(-4,0)的位置,即平移后所得图象与x轴的另一个交点的坐标为(-4,0).
(1)由题意得m﹣2=﹣3,
解得m=﹣1,
故二次函数的解析式为y=x2+2x﹣3;如图,
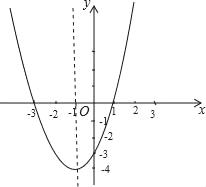
(2)令y=0,即x2+2x﹣3=0,解得 x1=﹣3,x2=1,
则二次函数图象与x轴的两个交点坐标分别为(﹣3,0)、(1,0),
故二次函数图象向左平移1个单位后经过坐标原点,平移后所得图象与x轴的另一个交点坐标为(﹣4,0).

练习册系列答案
相关题目