题目内容
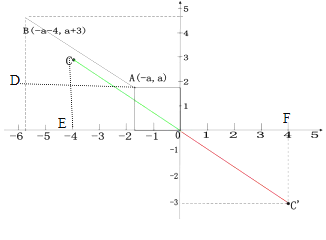
【题目】在平面直角坐标系中，O为坐标原点，点A(-a，a)(a>0)，点B(-a-4，a+3)，C为该直角坐标系内的一点，连结AB，OC．若AB∥OC且AB=OC，则点C的坐标为________
【答案】（-4,3），（4，-3）
【解析】
根据题意画出图形，由AB∥OC，AB=OC，易证△ABD≌△OCE≌△OFC， 可得出BD=CE，AD=OE，再根据点A、B的坐标求出AD、BD的长，根据点C的位置（在第二象限和第四象限），写出点C的坐标，即可求解.
如图
∵AB∥OC，AB=OC
易证△ABD≌△OCE≌△OFC
∴BD=CE，AD=OE
∵点A(-a，a)(a>0)，点B(-a-4，a+3)
∴AD=-a-（-a-4）=4，BD=a+3-a=3
∴OE=4，CE=3
∵点C在第二象限，
∴点C的坐标为（-4,3）
∵点C和点C关于原点对称
∴C的坐标为（4，-3）
故答案为：（-4,3），（4，-3）.
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
