Question

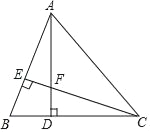
【题目】如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD=CD．

（1）求证：△ABD≌△CFD；

（2）已知BC=7，AD=5，求AF的长．

Answer 1

【答案】（1）证明见解析；（2）3.

【解析】

（1）易由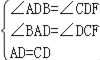，可证△ABD≌△CFD（AAS）；

（2）由△ABD≌△CFD，得BD=DF，所以BD=BC﹣CD=2，所以AF=AD﹣DF=5﹣2．

（1）证明：∵AD⊥BC，CE⊥AB，

∴∠ADB=∠CDF=∠CEB=90°，

∴∠BAD+∠B=∠FCD+∠B=90°，

∴∠BAD=∠OCD，

在△ABD和CFD中，

，

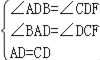∴△ABD≌△CFD（AAS），

（2）∵△ABD≌△CFD，

∴BD=DF，

∵BC=7，AD=DC=5，

∴BD=BC﹣CD=2，

∴AF=AD﹣DF=5﹣2=3．