题目内容
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)经过点A(4,﹣5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.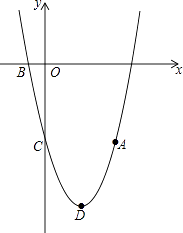
(1)求这条抛物线的表达式;
(2)连结AB、BC、CD、DA,求四边形ABCD的面积;
(3)如果点E在y轴的正半轴上,且∠BEO=∠ABC,求点E的坐标.
【答案】
(1)
解:∵抛物线y=ax2+bx﹣5与y轴交于点C,
∴C(0,﹣5),
∴OC=5.
∵OC=5OB,
∴OB=1,
又点B在x轴的负半轴上,
∴B(﹣1,0).
∵抛物线经过点A(4,﹣5)和点B(﹣1,0),
∴ ![]() ,解得
,解得 ![]() ,
,
∴这条抛物线的表达式为y=x2﹣4x﹣5.
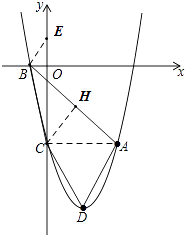
(2)
解:由y=x2﹣4x﹣5,得顶点D的坐标为(2,﹣9).
连接AC,
∵点A的坐标是(4,﹣5),点C的坐标是(0,﹣5),
又S△ABC= ![]() ×4×5=10,S△ACD=
×4×5=10,S△ACD= ![]() ×4×4=8,
×4×4=8,
∴S四边形ABCD=S△ABC+S△ACD=18.
(3)
解:过点C作CH⊥AB,垂足为点H.
∵S△ABC= ![]() ×AB×CH=10,AB=5
×AB×CH=10,AB=5 ![]() ,
,
∴CH=2 ![]() ,
,
在RT△BCH中,∠BHC=90°,BC= ![]() ,BH=
,BH= ![]() =3
=3 ![]() ,
,
∴tan∠CBH= ![]() =
= ![]() .
.
∵在RT△BOE中,∠BOE=90°,tan∠BEO= ![]() ,
,
∵∠BEO=∠ABC,
∴ ![]() ,得EO=
,得EO= ![]() ,
,
∴点E的坐标为(0, ![]() )
)
【解析】(1)先得出C点坐标,再由OC=5BO,得出B点坐标,将A、B两点坐标代入解析式求出a,b;(2)分别算出△ABC和△ACD的面积,相加即得四边形ABCD的面积;(3)由∠BEO=∠ABC可知,tan∠BEO=tan∠ABC,过C作AB边上的高CH,利用等面积法求出CH,从而算出tan∠ABC,而BO是已知的,从而利用tan∠BEO=tan∠ABC可求出EO长度,也就求出了E点坐标.
【考点精析】本题主要考查了二次函数的概念和二次函数的图象的相关知识点,需要掌握一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.

【题目】某商场销售甲、乙两种品牌的智能手机.这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4400 | 2000 |
售价(元/部) | 5000 | 2500 |
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.(毛利润=(售价一进价)×销售量)
(Ⅰ)该商场计划购进甲、乙两种手机各多少部?
(II)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过156万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润。
【题目】某工厂设门市部专卖某产品,该产品每件成本40元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
每件销售价(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
每天售出件数 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设当天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察这些统计数据,找出每天售出件数y与每件售价x(元)之间的函数关系,并写出该函数关系式.
(2)门市部原设有两名营业员,但当销售量较大时,在每天售出量超过168件时,则必须增派一名营业员才能保证营业有序进行,设营业员每人每天工资为40元.求每件产品应定价多少元,才能使每天门市部纯利润最大(纯利润指的是收入总价款扣除成本及营业员工资后的余额,其它开支不计)