题目内容
【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.

【答案】(1)证明见解析(2)四边形MPNQ是菱形.
【解析】证明:(1)∵四边形ABCD是矩形,
∵AB=CD,AD=BC,∠A=∠C=90°,
∵在矩形ABCD中,M、N分别是AD.BC的中点,
∴AM=![]() AD,CN=
AD,CN=![]() BC,
BC,
∴AM=CN,
在△MAB≌△NDC,
∵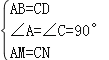 ,
,
∴△MAB≌△NDC;
(2)四边形MPNQ是菱形,
理由如下:连接AN,
易证:△ABN≌△BAM,
∴AN=BM,
∵△MAB≌△NDC,
∴BM=DN,
∵P、Q分别是BM、DN的中点,
∴PM=NQ,
∵DM=BN,DQ=BP,∠MDQ=∠NBP,
∴△MQD≌△NPB.
∴四边形MPNQ是平行四边形,
∵M是AB中点,Q是DN中点,
∴MQ=![]() AN,
AN,
∴MQ=![]() BM,
BM,
∴MP=![]() BM,
BM,
∴MP=MQ,
∴四边形MQNP是菱形.
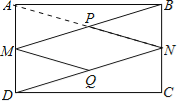
(1)根据矩形的性质和中点的定义,利用SAS判定△MBA≌△NDC;
(2)四边形MPNQ是菱形,连接AN,有(1)可得到BM=CN,再有中点得到PM=NQ,再通过证明△MQD≌△NPB得到MQ=PN,从而证明四边形MPNQ是平行四边形,利用三角形中位线的性质可得:MP=MQ,进而证明四边形MQNP是菱形.

练习册系列答案
相关题目