题目内容
【题目】在等腰三角形ABC中,AB=AC,D是AB延长线上一点,E是AC上一点,DE交BC于点F.
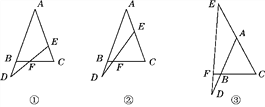
(1)如图①,若BD=CE,求证:DF=EF.
(2)如图②,若BD=![]() CE,试写出DF和EF之间的数量关系,并证明.
CE,试写出DF和EF之间的数量关系,并证明.
(3)如图③,在(2)的条件下,若点E在CA的延长线上,那么(2)中结论还成立吗?试证明.
【答案】(1)证明见解析;(2)DF=![]() EF.(3)成立,证明见解析.
EF.(3)成立,证明见解析.
【解析】试题分析:
(1)在题图①中作EG∥AB交BC于点G,利用平行线的性质和等腰三角形的性质可证得:EG=EC;再证△BFD≌△GFE即可;
(2)在题图②中作EG∥AB交BC于点G,则∠D=∠FEG.同(1)可得EG=EC;
再证△BFD∽△GFE,利用相似三角形的性质即可证得:DF=![]() EF.
EF.
(3)在题图③中作EG∥AB交CB的延长线于点G,同(2)证:EG=EC,△BFD∽△GFE,再利用相似三角形的性质可得:DF=![]() EF,即(2)中的结论任然成立
EF,即(2)中的结论任然成立
试题解析:
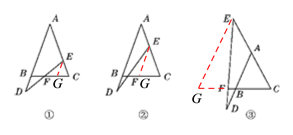
(1)在题图①中作EG∥AB交BC于点G,
则∠ABC=∠EGC,∠D=∠FEG.
∵AB=AC,∴∠ABC=∠C.
∴∠EGC=∠C.∴EG=EC.
∵BD=CE,∴BD=EG.
∵∠D=∠FEG,∠BFD=∠GFE,
∴△BFD≌△GFE.
∴DF=EF.
(2)解:DF=![]() EF.
EF.
在题图②中作EG∥AB交BC于点G,则∠D=∠FEG.由(1)得EG=EC.
∵∠D=∠FEG,∠BFD=∠EFG,
∴△BFD∽△GFE.
∴![]() .
.
∵BD=![]() CE=
CE=![]() EG,
EG,
∴DF=![]() EF.
EF.
(3)成立.
在题图③中作EG∥AB交CB的延长线于点G,
则仍有EG=EC,△BFD∽△GFE.
∴![]() ,
,
∵BD=![]() CE=
CE=![]() EG,
EG,
∴DF=![]() EF.
EF.

练习册系列答案
相关题目