题目内容
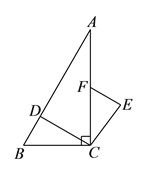
【题目】如图,在![]() 中,
中, ![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上, ![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后得
后得![]() ,连接
,连接![]() .
.
(![]() )求证:
)求证: ![]() ≌
≌![]() .
.
(![]() )若
)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(![]() )答案见解析.(
)答案见解析.(![]() )
)![]() .
.
【解析】试题分析:(1)由旋转的性质可得:CD=CE,再根据同角的余角相等可证明∠BCD=∠FCE,再根据全等三角形的判定方法即可证明△BCD≌△FCE;
(2)由(1)可知:△BCD≌△FCE,所以∠BDC=∠E,易求∠E=90°,进而可求出∠BDC的度数.
试题解析:解:(1)∵将线段CD绕点C按顺时针方向旋转90°后得CE,∴CD=CE,∠DCE=90°,∵∠ACB=90°,∴∠BCD=90°﹣∠ACD=∠FCE,在△BCD和△FCE中,∵CB=CF,∠BCD=∠FCE,CD=CE,∴△BCD≌△FCE(SAS).
(2)由(1)可知△BCD≌△FCE,∴∠BDC=∠E,∠BCD=∠FCE,∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,∵EF∥CD,∴∠E=180°﹣∠DCE=90°,∴∠BDC=90°.

练习册系列答案
相关题目
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和告知给你代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写表格;
平均数/分 | 中位数/分 | 众数/分 | |
初中代表队 | |||
高中代表队 |
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.