题目内容
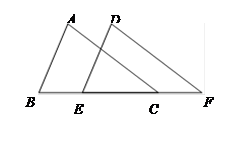
(本题满分6分)如图,已知点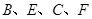 在同一直线上,
在同一直线上, ∥
∥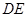 ,且
,且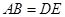 ,
,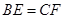 ,求证:
,求证: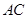 ∥
∥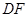 .
.
 在同一直线上,
在同一直线上, ∥
∥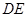 ,且
,且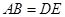 ,
,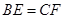 ,求证:
,求证: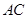 ∥
∥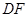 .
.
证明:∵ ∥
∥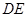 ,∴
,∴ ,∵
,∵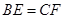 ,∴
,∴ 即
即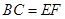 ,在△ABC和△DEF中,
,在△ABC和△DEF中,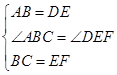 ,∴△ABC≌△DEF,∴
,∴△ABC≌△DEF,∴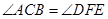 ,∴
,∴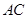 ∥
∥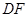
 ∥
∥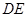 ,∴
,∴ ,∵
,∵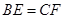 ,∴
,∴ 即
即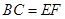 ,在△ABC和△DEF中,
,在△ABC和△DEF中,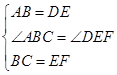 ,∴△ABC≌△DEF,∴
,∴△ABC≌△DEF,∴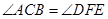 ,∴
,∴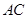 ∥
∥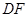
试题分析:先由两线段平行推出同位角相等,再由全等三角形推出对应角相等,接着由同位角相等反推出两线段平行
点评:本题较为简单,难度不大,只需证明出两个三角形全等,即可证明出其对应的角相等

练习册系列答案
相关题目
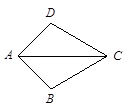
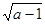 +b
+b -4b+4=0,求c的取值范围。
-4b+4=0,求c的取值范围。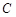 是
是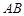 的中点,
的中点,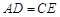 ,
,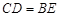 .求证:△
.求证:△ ≌△
≌△ .
.
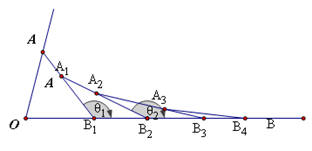
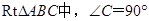 ,
,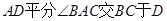 ,若
,若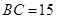 ,且
,且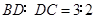 ,则
,则 到边
到边 的距离是 .
的距离是 . ∠B, 则下列能正确表示∠EAD ∠B、∠C之间的关系的是( ):
∠B, 则下列能正确表示∠EAD ∠B、∠C之间的关系的是( ):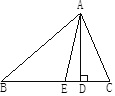
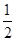 (∠C +∠B)
(∠C +∠B)