题目内容
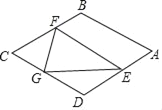
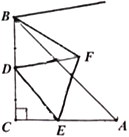
【题目】如图，在等腰直角三角形
中，
，
，
为
中点，
为
边上一动点，连接
，以为边并在的右侧作等边
，连接
，则的最小值为______.
【答案】3
【解析】
由60°联想旋转全等，转换动长为定点到定线的长，构建等边三角形BDG，利用△BDF≌△GDE，转换BF=GE，然后即可求得其最小值.
以BD为边作等边三角形BDG，连接GE，如图所示：
∵等边三角形BDG，等边三角形DEF
∴∠BDG=∠EDF=60°，BD=GD=BG，DE=DF=EF
∴∠BDG+∠GFD=∠EDF+∠GFD，即∠BDF=∠GDE
∴△BDF≌△GDE（SAS）
∴BF=GE
当GE⊥AC时，GE有最小值，如图所示GE′，作DH⊥GE′
∴BF=GE= CD+
DG=2+1=3
故答案为：3.
练习册系列答案
名校课堂系列答案
相关题目
