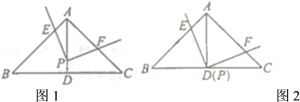
题目内容
【题目】如图，抛物线
与坐标轴相交于
、
、
三点，
是线段
上一动点（端点除外），过作
，交
于点
，连接
．
直接写出、、的坐标；
求抛物线的对称轴和顶点坐标；
求
面积的最大值，并判断当的面积取最大值时，以
、
为邻边的平行四边形是否为菱形．
【答案】（1）
、
、
．
对称轴是直线
，顶点坐标是
．（3）以
、
为邻边的平行四边形不是菱形．
【解析】
（1）设y=0，解一元二次方程即可求出A和B的坐标，设x=0，则可求出C的坐标．
（2）抛物线：
，所以抛物线的对称轴是直线x=1，顶点坐标是（1，﹣
）．
（3）设P（x，0）（﹣2＜x＜4），由PD∥AC，可得到关于PD的比例式，由此得到PD和x的关系，再求出C到PD的距离（即P到AC的距离），利用三角形的面积公式可得到S和x的函数关系，利用函数的性质即可求出三角形面积的最大值，进而得到x的值，所以PD可求，而PA≠PD，所以PA、PD为邻边的平行四边形不是菱形．
（1）A（4，0）、B（﹣2，0）、C（0，﹣4）．
（2）抛物线：，∴抛物线的对称轴是直线x=1，顶点坐标是（1，﹣）．
（3）设P（x，0）（﹣2＜x＜4）．
∵PD∥AC，∴
，解得：
．
∵C到PD的距离（即P到AC的距离）：
，∴△PCD的面积
，∴
，∴△PCD面积的最大值为3，当△PCD的面积取最大值时，x=1，PA=4﹣x=3，
，因为PA≠PD，所以以PA、PD为邻边的平行四边形不是菱形．
练习册系列答案
相关题目
【题目】二次函数
，
，
是常数，且
中的
与
的部分对应值如下表所示，则下列结论中，正确的个数有（ ）
|
|
|
|
|
|
|
|
|
|
；
当
时，
；
当
时，的值随值的增大而减小；
方程
有两个不相等的实数根．
A. 4个 B. 3个 C. 2个 D. 1个
