题目内容
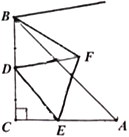
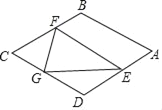
【题目】如图,在菱形ABCD中,AB=![]() ,∠B=120°,点E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为_____.
,∠B=120°,点E是AD边上的一个动点(不与A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.若△EFG是等腰三角形,则DE的长为_____.
【答案】1或![]()
【解析】
由四边形ABCD是菱形,得到BC∥AD,由于EF∥AB,得到四边形ABFE是平行四边形,根据平行四边形的性质得到EF∥AB,于是得到EF=AB=![]() ,当△EFG为等腰三角形时,①EF=GE=
,当△EFG为等腰三角形时,①EF=GE=![]() 时,于是得到DE=DG=
时,于是得到DE=DG=![]() AD÷
AD÷![]() =1,②GE=GF时,根据勾股定理得到DE=
=1,②GE=GF时,根据勾股定理得到DE=![]() .
.
∵四边形ABCD是菱形,∠B=120°,
∴∠D=∠B=120°,∠A=180°-120°=60°,BC∥AD,
∵EF∥AB,
∴四边形ABFE是平行四边形,
∴EF∥AB,
∴EF=AB=![]() ,∠DEF=∠A=60°,∠EFC=∠B=120°,
,∠DEF=∠A=60°,∠EFC=∠B=120°,
∵DE=DG,
∴∠DEG=∠DGE=30°,
∴∠FEG=30°,
当△EFG为等腰三角形时,
当EF=EG时,EG=![]() ,
,
如图1,
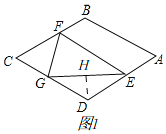
过点D作DH⊥EG于H,
∴EH=![]() EG=
EG=![]() ,
,
在Rt△DEH中,DE=![]() =1,
=1,
GE=GF时,如图2,
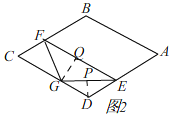
过点G作GQ⊥EF,
∴EQ=![]() EF=
EF=![]() ,在Rt△EQG中,∠QEG=30°,
,在Rt△EQG中,∠QEG=30°,
∴EG=1,
过点D作DP⊥EG于P,
∴PE=![]() EG=
EG=![]() ,
,
同①的方法得,DE=![]() ,
,
当EF=FG时,由∠EFG=180°-2×30°=120°=∠CFE,此时,点C和点G重合,点F和点B重合,不符合题意,
故答案为:1或![]() .
.

练习册系列答案
相关题目
【题目】二次函数![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 中的
中的![]() 与
与![]() 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )
|
|
|
|
|
|
|
|
|
|
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;
值的增大而减小;
![]() 方程
方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个