题目内容
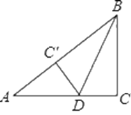
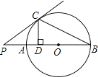
【题目】如图,![]() 为
为![]() 的切线,
的切线,![]() 为切点,
为切点,![]() 是过
是过![]() 点的割线,
点的割线,![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】![]() 的面积为
的面积为![]() .
.
【解析】
连接AC,由弦切角定理知∠PCA=∠B,易证得△PCA∽△PBC,得PC:PB=AC:AB,而AC:AB正好是tanB,由此可求出PB的长,进而可由切割线定理求出PA的长,也就得到了AB的长;在Rt△ACB中,易证得∠ACD=∠B,那么tanB=tan∠ACD,由此可得CD=2AD,BD=2CD,即BD=4AD,联立AD+BD=AB(AB的长已求得),即可得到AD、BD、CD的长,进而可由三角形的面积公式求出△BCD的面积.
解法一:连接![]() ,
,
∵![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,
上,
∴![]()
∵![]() 于点
于点![]() ,
,
∴![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
∵![]() 切
切![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() 切
切![]() 于点
于点![]() ,
,![]() 是
是![]() 的割线,
的割线,
∴根据切割线定理:![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,
即![]() 的面积为
的面积为![]() ,
,
解法二:同解法一,由![]() 得
得![]() ,
,
∵![]() ,
,
∴![]() ,
,
由切割线定理,得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
解得![]() ;(
;(![]() 同证法一)
同证法一)
∴![]() ,
,![]() ,
,
![]() .
.
即![]() 的面积为
的面积为![]() .
.

练习册系列答案
相关题目
【题目】二次函数![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 中的
中的![]() 与
与![]() 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )
|
|
|
|
|
|
|
|
|
|
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;
值的增大而减小;
![]() 方程
方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个