题目内容
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元.则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨元(为正整数),每个月的销售利润为元.
(1)求与的函数关系式并直接写出自变量的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
(1))根据题意可知y=﹣10(x﹣5.5)2+2402.5,0<x≤15;
(2)当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元;
(3)当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元.
解析试题分析:(1)根据题意可知y=﹣10(x﹣5.5)2+2402.5,0<x≤15;
(2)当x=5.5时y有最大值.
(3)设y=2200,解得x的值.然后分情况讨论解.
试题解析:(1)∵设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
∴上涨后每件商品的利润为(10+x)元,每月能销售(210﹣10x)件商品;
由题意得:y=(210﹣10x)(50+x﹣40)
=﹣10x2+110x+2100
=﹣10(x﹣5.5)2+2402.5(0<x≤15且x为整数);
(2)∵a=﹣10<0,
∴当x=5.5时,y有最大值2402.5.
∵0<x≤15,且x为整数,
当x=5时,50+x=55,y=2400(元),当x=6时,50+x=56,y=2400(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是2400元;
(3)当y=2200时,﹣10x2+110x+2100=2200,
解得:x1=1,x2=10.
∴当x=1时,50+x=51,当x=10时,50+x=60.
∴当售价定为每件51或60元,每个月的利润为2200元.
当售价不低于51或60元,每个月的利润为2200元.
当售价不低于51元且不高于60元且为整数时,每个月的利润不低于2200元(或当售价分别为51,52,53,54,55,56,57,58,59,60元时,每个月的利润不低于2200元).
考点:二次函数的应用.

已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如下表:
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
(2)当x为何值时,y有最小值,最小值是多少?
(3)若A(m,y1),B(m+2,y2)两点都在该函数的图象上,计算当m 取何值时,
 ?
? 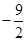 );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为( ,0),且BC=5,AC=3(如图1).
,0),且BC=5,AC=3(如图1).

 中,抛物线
中,抛物线 过点
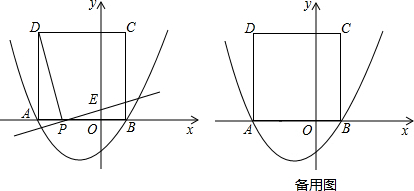
过点 ,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为
,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为 ,连接CA,CB,CD.
,连接CA,CB,CD.
 ;
; 是第一象限内抛物线上的一个动点,连接DP交BC于点E.
是第一象限内抛物线上的一个动点,连接DP交BC于点E. 的图像经过点
的图像经过点 和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.

 ,求抛物线的表达式;
,求抛物线的表达式; 相离、相切、相交.
相离、相切、相交. 的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(-3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.