题目内容
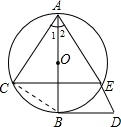
如图，AB为⊙O的直径，劣
=
弧BD∥CE，连接AE并延长交BD于D．
求证：
（1）BD是⊙O的切线；
（2）AB2=AC•AD．
 |
| BC |
|
| BE |
求证：
（1）BD是⊙O的切线；
（2）AB2=AC•AD．
证明：（1）∵
=
，
∴∠1=∠2，
=
，AC=AE．
∴AB⊥CE．
∵CE∥BD，∴AB⊥BD．
∴BD是⊙O的切线．
（2）连接CB．
∵AB是⊙O的直径，∴∠ACB=90°．
∵∠ABD=90°，∴∠ACB=∠ABD．
∵∠1=∠2，∴△ACB∽△ABD．
∴
=
，
∴AB2=AD•AC．
|
| CB |
|
| BE |
∴∠1=∠2，
|
| AC |
|
| AE |
∴AB⊥CE．
∵CE∥BD，∴AB⊥BD．
∴BD是⊙O的切线．
（2）连接CB．
∵AB是⊙O的直径，∴∠ACB=90°．
∵∠ABD=90°，∴∠ACB=∠ABD．
∵∠1=∠2，∴△ACB∽△ABD．
∴
| AC |
| AB |
| AB |
| AD |
∴AB2=AD•AC．
练习册系列答案
相关题目
△CPQ进行研究．
