题目内容
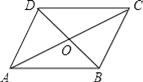
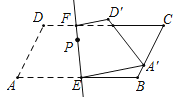
【题目】如图,直线EF分别交平行四边形ABCD边AB、CD于直E、F,将图形沿直线EF对折,点A、D分別落在点A′、D′处.若∠A=60°,AD=4,AB=8,当点A′落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA′的最小值( )
A.4+![]() B.8C.6+
B.8C.6+![]() D.4
D.4![]()
【答案】D
【解析】
连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.因为A、A′关于直线EF对称,推出P′A′=P′A,推出P′A′+P′C=P′A+P′C=AC,推出当点P与P′重合时,PA′+PC的值最小,最小值=AC的长;
如图,连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.
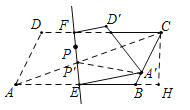
∵A、A′关于直线EF对称,
∴P′A′=P′A,
∴P′A′+P′C=P′A+P′C=AC,
∴当点P与P′重合时,PA′+PC的值最小,最小值=AC的长.
在Rt△BCH中,∵BC=4,∠CBH=60°,
∴BH=2,CH=2![]() ,
,
∴AH=AB+BH=10,
在Rt△ACH中,AC=![]() .
.
∴PC+PA′的最小值为![]() ,
,
故选:D.

练习册系列答案
相关题目