Question

【题目】若两个二次函数图象的顶点、开口方向都相同，则称这两个二次函数为“同簇二次函数”

（1）请直接写出两个为“同簇二次函数”的函数：①______，②_________；

（2）已知关于的二次函数和，若与为“同簇二次函数”，求函数的表达式，并求出当时，的最小值．

Answer 1

【答案】（1）①，②；（2），最小值为0

【解析】

（1）写出顶点在原点，开口方向向上的两个二次函数解析式即可；

（2）由，可得，再求出的顶点坐标，根据新定义得到二次函数的顶点坐标为，利用二次函数图象上点的坐标特征和对称轴方程解得，，则函数的表达式为，然后根据二次函数的性质求当时，的最小值．

解：（1）“两个为“同簇二次函数”的函数．①，②．

故答案为，．

（2）

则．

二次函数的顶点为，

与为“同簇二次函数”，

的顶点坐标为．

，

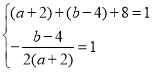解之，得：．

．

，

当时，．