Question

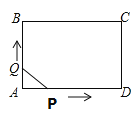
【题目】如图，抛物线y=ax2+bx过A(4，0) B(1，3)两点，点C 、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H

（1）求抛物线的解析式．

（2）直接写出点C的坐标，并求出△ABC的面积．

（3）点P是抛物线BA段上一动点，当△ABP的面积为3时，求出点P的坐标．

Answer 1

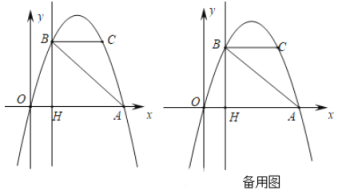
【答案】（1）y=-x2+4x；（2）点C的坐标为（3，3），3；（3）点P的坐标为（2，4）或（3，3）

【解析】

（1）将点A、B的坐标代入即可求出解析式；

（2）求出抛物线的对称轴，根据对称性得到点C的坐标，再利用面积公式即可得到三角形的面积；

（3）先求出直线AB的解析式，过P点作PE∥y轴交AB于点E，设其坐标为P（a，-a2+4a），得到点E的坐标为(a，-a+4)，求出线段PE，即可根据面积相加关系求出a，即可得到点P的坐标.

（1）把点A（4，0），B(1，3)代入抛物线y=ax2+bx中，得

，得，

∴抛物线的解析式为y=-x2+4x；

(2)∵，

∴对称轴是直线x=2，

∵B(1，3)，点C 、B关于抛物线的对称轴对称，

∴点C的坐标为（3，3），BC＝2，

点A的坐标是（4，0），BH⊥x轴，

∴S△ABC= =；

（3）设直线AB的解析式为y=mx+n，将B，A两点的坐标代入

得，解得，

∴y=-x+4，

过P点作PE∥y轴交AB于点E，P点在抛物线y=-x2+4x的AB段，

设其坐标为（a，-a2+4a），其中1<a<4，则点E的坐标为(a，-a+4)，

∴PE=(-a2+4a)-( -a+4)=-a2+5a-4，

∴S△ABP= S△PEB+ S△PEA=×PE×3=(-a2+5a-4)=，

得a1=2，a2=3，

P1(2，4)，P2(3，3)即点C，

综上所述，当△ABP的面积为3时，点P的坐标为（2，4）或（3，3）.