题目内容
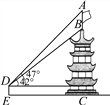
【题目】如图,某建筑物BC顶部有一旗杆AB,且点A、B、C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).(参考数据:tan47°≈1.07,tan42°≈0.90)
【答案】旗杆AB的高度约是3.6m,建筑物BC的高度约是20.5m.
【解析】试题分析:过点D作DF⊥AC,垂足为F,可得四边形DECF为矩形,即可得DF=EC=21,FC=DE=1.56.在Rt△DFA中,根据tan∠ADF=![]() 可求AF的长,在Rt△DFB中,根据tan∠BDF=
可求AF的长,在Rt△DFB中,根据tan∠BDF=![]() 可求BF的长,再由AB=AF-BF,BC=BF+FC即可求得旗杆AB的高度和建筑物BC的高度.
可求BF的长,再由AB=AF-BF,BC=BF+FC即可求得旗杆AB的高度和建筑物BC的高度.
试题解析:
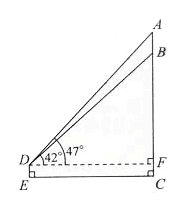
解:如图,根据题意,DE=1.56,EC="21," ∠ACE=90°, ∠DEC=90°.
过点D作DF⊥AC,垂足为F.
则∠DFC=90°, ∠ADF=47°, ∠BFD=42°.
可得四边形DECF为矩形.
∴DF=EC=21,FC=DE=1.56.
在Rt△DFA中,tan∠ADF=![]() .
.
∴AF=DF·tan47°≈21×1.07=22.47.
在Rt△DFB中,tan∠BDF=![]() .
.
∴BF=DF·tan42°≈21×0.90=18.90.
于是,AB=AF-BF=22.47-18.90=3.57≈3.6,
BC=BF+FC=18.90+1.56=20.46≈20.5.
答:旗杆AB的高度约为3.6m,建筑物BC的高度约为20.5m.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目