题目内容
【题目】如图1,在四边形ABCD中,AB∥CD,∠ABC=90°,动点P从A点出发,沿A→D→C→B匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
⑴①AD= , CD= , BC= ; (填空)
②当点P运动的路程x=8时,△ABP的面积为y= ; (填空)
⑵求四边形ABCD的面积
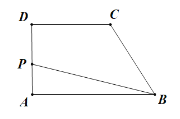
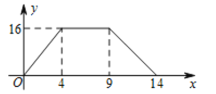
图1 图2
【答案】(1)①4,5,5;②16;(2)面积为26.
【解析】
(1)①根据图2的图像,当点P运动到点D时,运动距离是4,即可知道AD的长度,进而知道CD、BC的长度;②点P运动的路程是8时,点P在CD上,即可得到△ABP的面积;
(2)根据(1)所得的结论,可以求得AB的长度,进而计算四边形ABCD的面积.
(1)①根据函数图像可知:AD=4,CD=5,BC=5;
故答案为:4,5,5.
②当点P运动到CD上时,△ABP的面积达到最大值,
∴x=8时,△ABP的面积为16;
故答案为:16.
(2)当点P运动到点D时,有△ABP的面积为16,
∴![]() ,
,
∴AB=8
∴四边形ABCD的面积为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.