题目内容
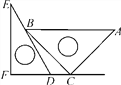
【题目】如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列式子不成立的是( )

A. DA=DEB. BD=CEC. ∠EAC=90°D. ∠ABC=2∠E
【答案】B
【解析】
依题意推出∠OAD+∠ODA=90°,四边形ABDE是平行四边形,然后基于推论得出AB=DA=DE,∠E=∠ABD,∠EAD+∠ODA=90°,则∠EAC=90°,∠ABC=2∠E.
解:∵四边形ABCD是菱形
∴AB∥CE,AB=DA=DC=BC,∠ABC=2∠ABD,BD⊥AC
∴∠OAD+∠ODA=90°
又∵BD∥AE,∴四边形ABDE是平行四边形,∠EAD=∠OAD
∴AB=DA=DE,∠E=∠ABD
∴∠EAD+∠ODA=90°
即∠EAC=90°,∠ABC=2∠E,故不成立的是B.
故选B.
此题主要考查菱形的基本性质:菱形的四条边都相等;菱形的对角线互相垂直平分,且每一条对角线平分一组对角.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目