��Ŀ����
����Ŀ����ͼ����·![]() Ϊ���������ڵ�
Ϊ���������ڵ�![]() ��ƫ��
��ƫ��![]() �����ϣ�����
�����ϣ�����![]() ǧ�״��Ǵ�ׯ
ǧ�״��Ǵ�ׯ![]() ���ڵ�
���ڵ�![]() ��ƫ��
��ƫ��![]() �����ϣ�����
�����ϣ�����![]() ǧ�״��Ǵ�ׯ
ǧ�״��Ǵ�ׯ![]() ��Ҫ�ڹ�·
��Ҫ�ڹ�·![]() ����һ�����ز��չ�վ
����һ�����ز��չ�վ![]() (ȡ��
(ȡ��![]() ��
��![]() ��)��ʹ��
��)��ʹ��![]() ��
��![]() ����ׯ��
����ׯ��![]() վ�ľ���֮����̣�����ͼ������
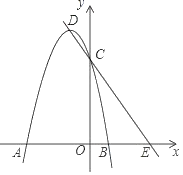
վ�ľ���֮����̣�����ͼ������![]() ��λ�ã���д�����������㣺
��λ�ã���д�����������㣺
��1��![]() ��
��![]() ����ׯ֮��ľ��룻
����ׯ֮��ľ��룻
��2��![]() ��
��![]() ��
��![]() ����֮�͵���Сֵ.���ο����ݣ�sin36.5����0.6��cos36.5����0.8��tan36.5����0.75��������������.��
����֮�͵���Сֵ.���ο����ݣ�sin36.5����0.6��cos36.5����0.8��tan36.5����0.75��������������.��

���𰸡�(1) M��N����ׯ֮��ľ���Ϊ![]() ǧ��;(2) ��ׯM��N��Pվ����̾������5
ǧ��;(2) ��ׯM��N��Pվ����̾������5![]() ǧ�ף�
ǧ�ף�
��������
��1����N����AB�ĶԳƵ�N'��AB����E������MN����AB����P����PΪ���ز��չ�վ��λ�ã����DN��DM�����ù��ɶ������ɽ�����⣮
��2���������֪��M��N��AB�ϵ�P�ľ���֮����̳��Ⱦ���MN���ij���
�⣺��N����AB�ĶԳƵ�N'��AB����E������MN����AB����P����PΪ���ز��չ�վ��λ�ã�

��1����Rt��ANE��AN=10����NAB=36.5��
��NE=ANsin��NAB=10sin36.5��=6��
AE=ANcos��NAB=10cos36.5��=8��
��M��MC��AB�ڵ�C��
��Rt��MAC��AM=5����MAB=53.5��
��AC=MAsin��AMB=MAsin36.5��=3��
MC=MAcos��AMC=MAcos36.5��=4��
����M��MD��NE�ڵ�D��
��Rt��MND��MD=AE-AC=5��
ND=NE-MC=2��
��MN=![]() =
=![]() ��
��
��M��N����ׯ֮��ľ���Ϊ![]() ǧ�ף�
ǧ�ף�
��2���������֪��M��N��AB�ϵ�P�ľ���֮����̳��Ⱦ���MN���ij���
DN��=10��MD=5����Rt��MDN���У��ɹ��ɶ�������
MN��=![]() =5
=5![]() ��ǧ�ף�
��ǧ�ף�
���ׯM��N��Pվ����̾������5![]() ǧ�ף�
ǧ�ף�