题目内容
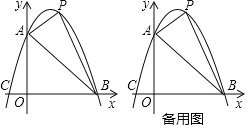
【题目】如图,在⊙O中,AB是直径,AD是弦,∠ADE = 60°,∠C = 30°.
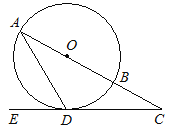
⑴判断直线CD是否是⊙O的切线,并说明理由;
⑵若CD = ![]() ,求BC的长.
,求BC的长.
【答案】(1)CD是⊙O的切线.
证明:如图,连接OD.
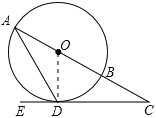
∵∠ADE=60°,∠C=30°,∴∠A=30°.
∵OA=OD,∴∠ODA=∠A=30°.
∴∠ODE=∠ODA+∠ADE=30°+60°=90°,∴OD⊥CD.
∴CD是⊙O的切线.
(2)解:在Rt△ODC中,∠ODC=90°, ∠C=30°, CD=![]() .
.
∵tanC=![]() ,
,
∴OD=CD·tanC=![]() ×
×![]() =3.
=3.
∴OC=2OD =6.
∵OB=OD=3,∴BC=OC-OB=6-3=3.
【解析】(1)根据切线的判定定理,连接OD,只需证明OD⊥CD,根据三角形的外角的性质得∠A=30°,再根据等边对等角得∠ADO=∠A,从而证明结论;
(2)在30°的直角三角形OCD中,求得OD,OC的长,则BC=OC-OB.

练习册系列答案
相关题目
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①② B. ①③ C. ①②③ D. ①③④