题目内容
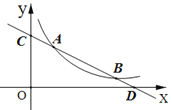
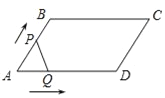
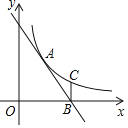
【题目】如图，反比例函数y=
（x＞0）的图象与直线AB交于点A（2，3），直线AB与x轴交于点B（4，0），过点B作x轴的垂线BC，交反比例函数的图象于点C，在平面内存在点D，使得以A，B，C，D四点为顶点的四边形为平行四边形，则点D的坐标是______．
【答案】（2，
）或（2，
）或（6，-）
【解析】
先将A点的坐标代入反比例函数求得k的值，然后将x=4代入反比例函数解析式求得相应的y的值，即得点C的坐标；然后结合图象分类讨论以A、B、C、D为顶点的平行四边形，如图所示，找出满足题意的D的坐标即可．
解：把点A（2，3）代入y=
（x＞0）得：k=xy=6，
故该反比例函数解析式为：y=
．
∵点B（4，0），BC⊥x轴，
∴把x=4代入反比例函数y=，得
y=
．
则C（4，）．
①如图，当四边形ACBD为平行四边形时，AD∥BC且AD=BC．
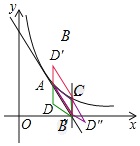
∵A（2，3）、B（4，0）、C（4，），
∴点D的横坐标为2，yA-yD=yC-yB，故yD=．
所以D（2，）．
②如图，当四边形ABCD′为平行四边形时，AD′∥CB且AD′=CB．
∵A（2，3）、B（4，0）、C（4，），
∴点D的横坐标为2，yD′-yA=yC-yB，故yD′=
．
所以D′（2，）．
③如图，当四边形ABD″C为平行四边形时，AC=BD″且AC∥BD″．
∵A（2，3）、B（4，0）、C（4，），
∴xD″-xB=xC-xA即xD″-4=4-2，故xD″=6．
yD″-yB=yC-yA即yD″-0=-3，故yD″=-．
所以D″（6，-）．
综上所述，符合条件的点D的坐标是：（2，）或（2，）或（6，-）．
故答案为（2，）或（2，）或（6，-）．
阅读快车系列答案
【题目】某校初二年级数学考试，（满分为100分，该班学生成绩均不低于50分）作了统计分析，绘制成如图频数分布直方图和频数、频率分布表，请你根据图表提供的信息，解答下列问题：
分组 | 49.5～59.5 | 59.5～69.5 | 69.5～79.5 | 79.5～89.5 | 89.5～100.5 | 合计 |
频数 | 2 | a | 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
（1）频数、频率分布表中a= ，b= ；（答案直接填在题中横线上）
（2）补全频数分布直方图；
（3）若该校八年级共有600名学生，且各个班级学生成绩分布基本相同，请估计该校八年级上学期期末考试成绩低于70分的学生人数．
