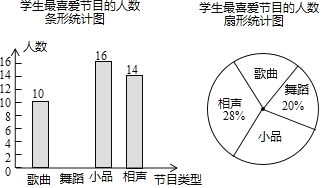
��Ŀ����
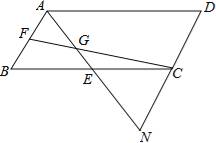
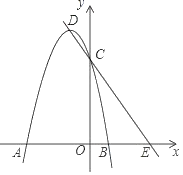
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+2ax��3a��a��0����x���ཻ��A��B������y���ཻ�ڵ�C������ΪD��ֱ��DC��x���ཻ�ڵ�E��
��1����a����1ʱ�������߶���D������Ϊ�� ����OE���� ����
��2��OE�ij��Ƿ���aֵ�йأ�˵��������ɣ�
��3�����DEO������������30�����ӵ�60��Ĺ����У���D�˶���·������
��4����DEΪб�ߣ���ֱ��DE�����Ϸ�������Rt��PDE����P��m��n������ֱ��д��n����m�ĺ�������ʽ���Ա���m��ȡֵ��Χ��
���𰸡���1������1��4����3��2��OE�ij���aֵ�أ�3��![]() ��4��n��m+1��m����1��
��4��n��m+1��m����1��
��������
��1�����ֱ��CD�Ľ���ʽ���ɽ�����⣻
��2�����ò���a�����ֱ��CD�Ľ���ʽ�����E���꼴���жϣ�
��3������������������µ�a��ֵ���ɵ�D�˶���·������
��4����ͼ����PM�ͶԳ�����M��PN��AB��N������ȫ�������ε����ʼ��ɽ�����⣮
��1����a����1ʱ�������ߵĽ���ʽΪy����x2��2x+3��
�ඥ��D����1��4����C��0��3����
��ֱ��CD�Ľ���ʽΪy����x+3��
��E��3��0����
��OE��3��
�ʴ�Ϊ������1��4����3��
��2�����ۣ�OE�ij���aֵ�أ�
���ɣ���y��ax2+2ax��3a��
��C��0����3a����D����1����4a����
��ֱ��CD�Ľ���ʽΪy��ax��3a��
��y��0ʱ��x��3��
��E��3��0����
��OE��3��
��OE�ij���aֵ�أ�
��3����ͼ��
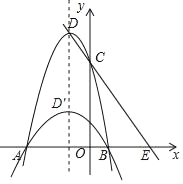
������30��ʱ��OC��![]() OE��
OE��![]() ��
��
�ੁ3a��![]() ��
��
��a����![]() ����ʱ��D��������ǣ���1��
����ʱ��D��������ǣ���1��![]() ����
����
������60��ʱ����Rt��OCE�У�OC��![]() OE��3
OE��3![]() ��
��
�ੁ3a��3![]() ��
��
��a����![]() ����ʱ��D�������ǣ���1��4
����ʱ��D�������ǣ���1��4![]() ����
����
���D�˶���·����Ϊ��4![]() ��
��![]() ��
��![]() ��
��
��4����ͼ����PM�ͶԳ�����M��PN��x����N��
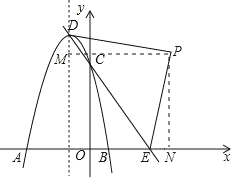
��PD��PE����PMD����PNE��90�㣬��DPE����MPN��90�㣬
���DPM����EPN��
���DPM�ա�EPN��AAS����
��PM��PN��DM��EN��
��D����1����4a����E��3��0����
����PM��PN�õ���n��m+1��
��DM��EN�õ���m��3����4a��n��
������D��x����ʱ��P��1��2������ʱm��ֵ1��
�������ߵĶ����ڵڶ����ޣ�
��m����1��
��n��m+1��m����1����