��Ŀ����
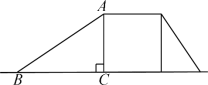
����Ŀ����֪��������OABC�ı�OC��OA�ֱ���x��y����������ϣ����B��4��4������P��t��0����x����һ���㣬����O��OH��AP�ڵ�H��ֱ��OH��ֱ��BC�ڵ�D����AD��
��1����ͼ1������P���߶�OC��ʱ����֤��OP��CD��
��2���ڵ�P�˶������У���AOP����A��B��DΪ���������������ʱ����t��ֵ��
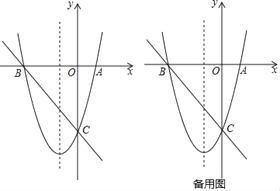
��3����ͼ2��������y����![]() x2+
x2+![]() x+4���Ƿ���ڵ�Q��ʹ����P��D��Q��CΪ������ı���Ϊƽ���ı��Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
x+4���Ƿ���ڵ�Q��ʹ����P��D��Q��CΪ������ı���Ϊƽ���ı��Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
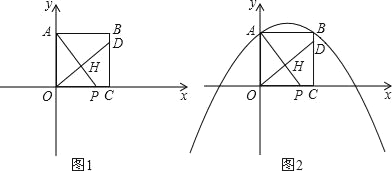
���𰸡�(1)������;(2) ���ϣ�t1��2��t2��![]() ��t3��
��t3��![]() ;(3)������.
;(3)������.
��������
��1��֤![]() ������֤���������ڵ�������ȫ�ȣ���֤����
������֤���������ڵ�������ȫ�ȣ���֤����![]() ����֪�������У�
����֪�������У�![]() ��
��![]() ��ֻ�����ҳ�һ���Ӧ����ȼ��ɣ�ͨ��ͼʾ���Է���
��ֻ�����ҳ�һ���Ӧ����ȼ��ɣ�ͨ��ͼʾ���Է���![]() ��
��![]() ��ͬ�ǵ���ǣ�����������ȣ���ô֤��������ȫ�ȵ�ȫ���������ѵó�������ۿ�֤��
��ͬ�ǵ���ǣ�����������ȣ���ô֤��������ȫ�ȵ�ȫ���������ѵó�������ۿ�֤��
��2����![]() ��
��![]() �����˶�����ô���������������ۣ�
�����˶�����ô���������������ۣ�
�ٵ�![]() ��
��![]() �Ḻ�����ϣ�����������1���Ľ���˼·����֤��
�Ḻ�����ϣ�����������1���Ľ���˼·����֤��![]() ��
��![]() ȫ�ȣ���ô�õ���������
ȫ�ȣ���ô�õ���������![]() ��Ȼ����
��Ȼ����![]() ��ʾ
��ʾ![]() ��
��![]() �ij����ٸ��ݸ��������������εõ��ı����߶Σ��е�ʽ�����ʱ
�ij����ٸ��ݸ��������������εõ��ı����߶Σ��е�ʽ�����ʱ![]() ��ֵ��Ҫע��
��ֵ��Ҫע��![]() ������ֵ���жϣ�
������ֵ���жϣ�
�ڵ�![]() ���߶�
���߶�![]() ��ʱ������
��ʱ������![]() ��
��![]() ��С�ڵ��������εı߳�����
��С�ڵ��������εı߳�����![]() ��
��![]() ��������ֻ��
��������ֻ��![]() ʱ�����������������β��п������ƣ���ʱ��ȫ�ȣ����ɾݴ����
ʱ�����������������β��п������ƣ���ʱ��ȫ�ȣ����ɾݴ����![]() ��ֵ��
��ֵ��
�۵�![]() �ڵ�
�ڵ�![]() ���Ҳ�ʱ������ͬ�٣�
���Ҳ�ʱ������ͬ�٣�
��3�������Ҫ������������ۣ�
���߶�![]() Ϊƽ���ı��εĶԽ��ߣ���ô��
Ϊƽ���ı��εĶԽ��ߣ���ô��![]() ��
��![]() ����
����![]() ���е�ԳƼ�����������껥Ϊ�෴������
���е�ԳƼ�����������껥Ϊ�෴������![]() ����
����![]() ��
��![]() �ĺ�������ͬ����ô����
�ĺ�������ͬ����ô����![]() ��ʾ��
��ʾ��![]() ������꣬���������ߵĽ���ʽ�У�����ȷ��
������꣬���������ߵĽ���ʽ�У�����ȷ��![]() ��ֵ��
��ֵ��
���߶�![]() Ϊƽ���ı��εıߣ�����
Ϊƽ���ı��εıߣ�����![]() ��ʾ��
��ʾ��![]() �ij����ѵ�
�ij����ѵ�![]() ���������ƽ��
���������ƽ��![]() ������λ���ܱ������
������λ���ܱ������![]() �����꣬���������߽���ʽ�ɵõ�
�����꣬���������߽���ʽ�ɵõ�![]() ��ֵ.
��ֵ.
��1��֤������OD��AH��
���OAP����DOC��90�㩁��AOD��
������OABC�У�OA��OC��4����AOP����OCD��90�㣬����
�� ��
��
���AOP�ա�OCD
��OP��CD��
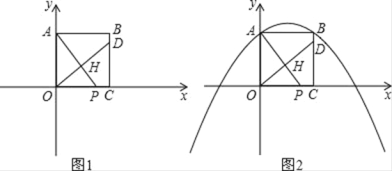
��2���⣺�ٵ�P��x�Ḻ������ʱ��P��t��0������t��0����ͼ�٣�
����Rt��AOP��OH��AP��
���POH����PAO��90�㩁��APO��
�֡ߡ�POH����COD��
���COD����PAO��
�ڡ�AOP���OCD�У�
�� ��
��
���AOP�ա�OCD��
��OP��CD����t����BD��BC+CD��4��t��
����AOP����A��B��DΪ��������������ƣ����У�
![]() ���ã�
���ã�![]() ��
��
��ã�![]() ��
��![]() ����ֵ��ȥ����
����ֵ��ȥ����
�ڵ���P���߶�OC��ʱ��P��t��0����0��t��4����ͼ�ڣ�
��ΪOP��OA��BD��AB��OA��AB��
����AOP����A��B��DΪ��������������ƣ���ô�У�![]() ������OP��BD������
������OP��BD������
t��4��t��t��2��
�۵���P�ڵ�C�Ҳ�ʱ��P��t��0����t��4����ͼ�ۣ�
ͬ�ٿ����![]() ��
��
���ϣ�t1��2��![]() ��
��![]() ��
��
��3���⣺������ڷ��������ĵ�Q��������������ۣ�
��PCΪƽ���ı��εĶԽ��ߣ���QP��CD����QP��CD��
��P��t��0����D��4��t������Q��t����t��������������![]() �У��ã�
�У��ã�
![]() ������t2��10t��24��0��
������t2��10t��24��0��
��ã�t1����2��t2��12��
��PCΪƽ���ı��εıߣ���DQ��PC����QD��PC��
��P��t��0����D��4��t������ PC��QD��|t��4|��Q��t��t����8��t��t����
Q��t��t��ʱ��![]() ������t2+2t��24��0��
������t2+2t��24��0��
��� t1��4���ᣩ��t2����6��
Q��8��t��t��ʱ��![]() ������t2��6t+8��0��
������t2��6t+8��0��
��� t1��4���ᣩ��t2��2��
���Ͽ�֪��t1��2��t2��12��t3����6��t4����2��
����ڵ�Q��ʹ����P��D��Q��CΪ������ı���Ϊƽ���ı��Σ�