Question

【题目】（操作发现）

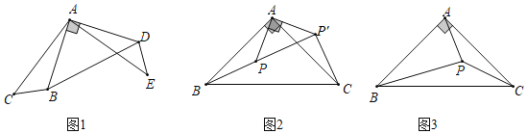
（1）如图1，将△ABC绕点A逆时针旋转90°得到△ADE，连接BD，则∠ABD的度数是______．

（类比探究）

（2）如图2，在等腰直角三角形ABC内取一点P，使∠APB=135°，将△ABP绕顶点A逆时针旋转90°得到△ACP'，连接PP'．请猜想BP与CP'有怎样的位置关系，并说明理由．

（解决问题）

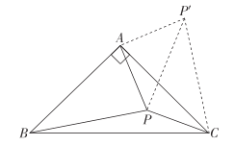
（3）如图3，在等腰直角三角形ABC内任取一点P，连接PA、PB、PC．求证：PC+PA＞PB．

Answer 1

【答案】(1)；(2)，理由见解析；(3) 见解析．

【解析】

（1）由题意可知AB=AD, ∠BAD=90°,所以可求∠ABD的度数;

（2）根据旋转得出△ACP′≌△ABP，根据全等得出∠AP′C=∠APB=1350，由(1)可知∠AP’P=450，求出∠BP’C=900即可．

(3) 将绕顶点逆时针旋转得到.在中，，即可证得.

(1) 由题意可知AB=AD, ∠BAD=90°,

∴∠ABD =．

(2)．

理由：∵绕顶点逆时针旋转得到，

∴，，，

∴．

∴，

∴，

∴点、、在同一直线上．

∵，，

∴，

∴．

(3)如图，将绕顶点逆时针旋转得到，

∴，

∴，，

连接，∵，

∴．

在中，，

∴．