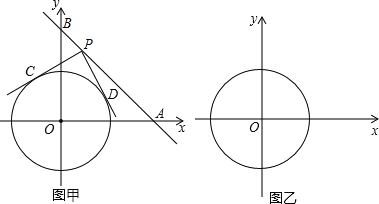
题目内容
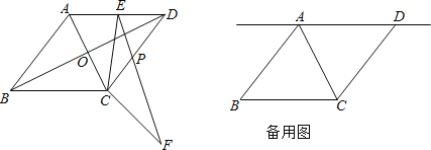
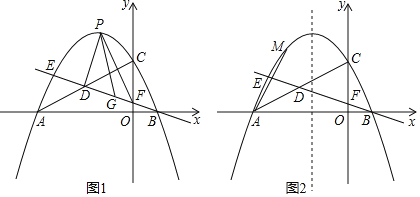
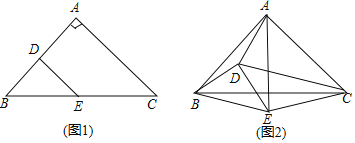
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC=2,点D、E分别是AB、BC的中点,把△BDE绕点B旋转,连接AD、AE、CD、CE,如图2.
(1)求证:△BDE∽△BAC.
(2)求△ABE面积最大时,△ADE的面积.
(3)在旋转过程中,当点D落在△ACE的边所在直线上时,直接写出CE的长.
【答案】(1)证明见解析;(2)![]() ;(3)满足条件的CE的值为
;(3)满足条件的CE的值为![]() 或
或![]() +1或
+1或![]() ﹣1.
﹣1.
【解析】
![]() 1)利用三角形的中位线定理即可解决问题.
1)利用三角形的中位线定理即可解决问题.![]() 当
当![]() 时,
时,![]() 的面积最大,根据
的面积最大,根据![]() 求解即可.
求解即可.
![]() 分4种情形:
分4种情形:![]() 如图
如图![]() 中,当点D在线段AE上时,
中,当点D在线段AE上时,![]() 如图
如图![]() 中,当点D在线段CE上,分别求解即可.
中,当点D在线段CE上,分别求解即可.![]() 如图
如图![]() 中,当点D在AE的延长线上时.
中,当点D在AE的延长线上时.![]() 如图
如图![]() 中,当点D在CE的延长线上时,分别求解即可.
中,当点D在CE的延长线上时,分别求解即可.
解:(1)如图1中,
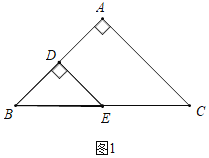
∵点D、E分别是AB、BC的中点,
∴DE∥AC,
∴△BDE∽△BAC.
(2)如图2中,作AH⊥BC于H.
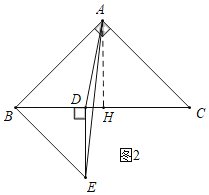
当EB⊥AB时,△ABE的面积最大,
S△ADE=S△ABE﹣S△BDE﹣S△ADB=![]() .
.
(3)如图3﹣2中,当点D在AE上时,
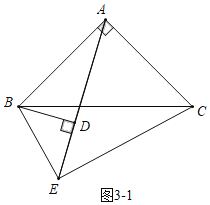
∵∠ABC=∠DBE=45°,
∴∠ABD=∠CBE,
![]() ,
,
∴△ABD∽△CBE,
∴∠ADB=∠BEC=90°,
∴EC=![]() .
.
如图3﹣2中,当点D在线段CE上,
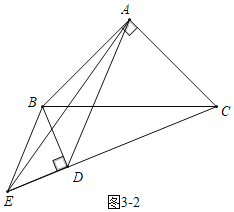
在Rt△BDC中,CD=![]() ,
,
∴EC=1+![]() .
.
如图3﹣3中,当点D在AE的延长线上时,易证∠BEC=90°,CE=![]()
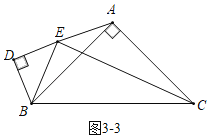
如图3﹣4中,当点D在CE的延长线上时,
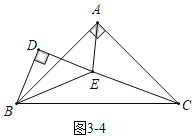
在Rt△BCD中,CD=![]() ,,
,,
∴EC=![]() ﹣1
﹣1
综上所述,满足条件的CE的值为![]() 或
或![]() +1或
+1或![]() ﹣1.
﹣1.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目