Question

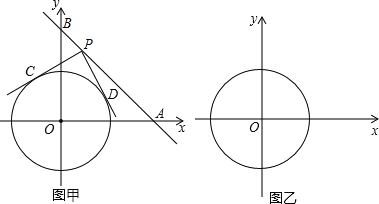
【题目】如图甲，在平面直角坐标系中，直线分别交x轴、y轴于点A、B，⊙O的半径为个单位长度，点P为直线y＝﹣x+6上的动点，过点P作⊙O的切线PC、PD，切点分别为C、D，且PC⊥PD．

（1）判断四边形OCPD的形状并说明理由．

（2）求点P的坐标．

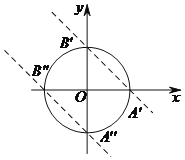
（3）若直线y＝﹣x+6沿x轴向左平移得到一条新的直线y1＝﹣x+b，此直线将⊙O的圆周分得两段弧长之比为1：3，请直接写出b的值．

（4）若将⊙O沿x轴向右平移（圆心O始终保持在x轴上），试写出当⊙O与直线y＝﹣x+6有交点时圆心O的横坐标m的取值范围．（直接写出答案）

Answer 1

【答案】（1）四边形OCPD为正方形，见解析；（2）P点坐标为(2，4)或(4，2)；（3）b的值为或；（4）

【解析】

（1）根据切线的性质得OC⊥PC，PD⊥PD，加上PC⊥PD，则可判断四边形OCPD为矩形，然后利用OC＝OD可判断四边形OCPD为正方形；

（2）利用正方形的性质得，利用勾股定理建立方程，解方程即可得出结论；

（3）利用直线y1＝﹣x+b将⊙O的圆周分得两段弧长之比为1：3可得到直线y1＝kx+b与坐标的交点A和点B为⊙O与坐标的交点，然后讨论：当点A和点B都在坐标轴的正半轴上或当点A和点B都在坐标轴的负半轴上时，易得b的值为±；

（4）先确定A点和B点坐标，再判断△OAB为等腰直角三角形，则∠ABO＝45°，然后讨论：当圆移动到点O1时与直线AB相切，作O1M⊥AB，如图丙，根据切线的性质得O1M＝，利用等腰直角三角形的性质得求出O1与O'2的坐标，于是根据直线与圆的位置关系可得到⊙O与直线y＝﹣x+6有交点时圆心O的横坐标m的取值范围．

解：（1）四边形OCPD为正方形．

理由如下：连接OC、OD，易知OC⊥PC，OD⊥PD，

又PC⊥PD，

∴四边形OCPD为矩形，

又OC＝OD，

∴四边形OCPD为正方形．

（2）连接OP，

为正方形，

，

在直线上，

设，

由得：，

解得：或．

点坐标为或．

（3）平移后的新直线A′B′交圆于A′B′，分得的两段弧长之比为1：3，

分得的劣弧是圆周的，

直线AB与x轴夹角为，，

，

当为圆周时，直线与坐标轴的交点恰好是与坐标轴的交点，

当AB平移到位置时，；

当AB平移到位置时，，

的值为或．

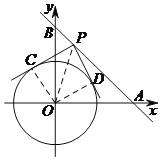
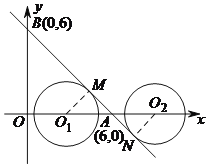
（4）如图，⊙O沿x轴向右平移过程中分别在⊙O1处，⊙O2处与直线y＝﹣x+6相切，

则圆在O落在O1，O2之间均满足题意，

在处相切时，为等腰直角三角形，

，．

，同理，在处相切时，，

，

当与直线有交点时，圆心O的横坐标m的取值范围为．