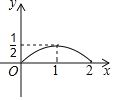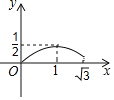题目内容
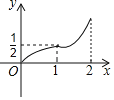
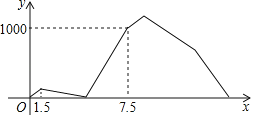
【题目】甲乙两人从A地出发去相距1800米的B地，甲出发1.5分钟后乙再出发，在中途乙追上甲，追上甲后，乙发现有东西忘带了，于是以原来1.2倍的速度返回，甲则继续以原速度前行，乙返回A地后取东西花了2分钟，取完东西后立即以返回时的速度追甲，甲达到B地以后立即返回，并与乙在途中相遇，设甲乙两人之间的距离为y(米)，甲出发的时间为x(分钟)，y与x的关系如图所示，则当甲乙两人第二次相遇时，两人距B地的距离为_____米．
【答案】
【解析】
由题意，甲的速度为1000÷7.5＝
米/分，再根据路程的关系求得乙返回时的速度为
米/分，根据相遇问题中的数量关系得到甲、乙两人最后相遇时，乙距B地的路程．
解：设乙原来的速度为a米/分，b分时，乙第一次追上甲，
由图可知：7.5分时，乙取东西返回时到A地，此时，甲、乙相距1000米，即甲7.5分走了1000米，
∴甲的速度是：
（米/分），
根据题意得：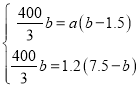
，
解得：a（b﹣1.5）＝1.2a（7.5﹣b），
b＝
，1.2a＝，
即乙返回时的速度为米/分，
设甲和乙第二次相遇的时间为m分，
（m﹣7.5﹣2）×+（m﹣7.5）×＝1800+1800﹣1000，
m＝
，
1800﹣（﹣7.5﹣2）×＝．
则当甲乙两人第二次相遇时，两人距B地的距离为米．
故答案为：．
练习册系列答案
相关题目
