��Ŀ����
����Ŀ����֪���ڡ�ABC�У�AB=AC����A���ֱ��a�����AC�غϵ�λ�ÿ�ʼ�Ƶ�A��˳ʱ�뷽����ת�Ǧȣ�ֱ��a��BC���ڵ�P����P�����B����C�غϣ�����BMN�ı�MNʼ����ֱ��a�ϣ���M�ڵ�N���Ϸ�������BM=BN������CN�� 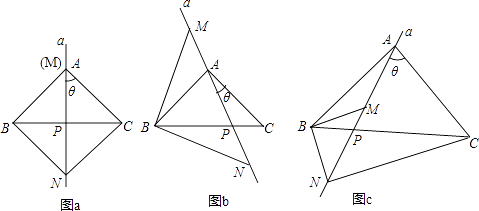
��1������BAC=��MBN=90��ʱ�� ����ͼa������=45��ʱ����ANC�Ķ���Ϊ��
��2������ͼb�����ȡ�45��ʱ�����еĽ����Ƿ����仯��˵�����ɣ�
��3����ͼc������BAC=��MBN��90��ʱ����ֱ��д����ANC���BAC֮���������ϵ������֤����
���𰸡�
��1��45��
��2���⣺����CN�����ȡ�45��ʱ�����еĽ��۲������仯��
�������£��ߡ�BAC=��MBN=90�㣬AB=AC��BM=BN��
���ABC=��ACB=��BNP=45�㣬
�֡ߡ�BPN=��APC��
���BNP�ס�ACP��
�� ![]() =
= ![]() ��
��
�֡ߡ�APB=��CPN��
���ABP�ס�CNP��
���ANC=��ABC=45��
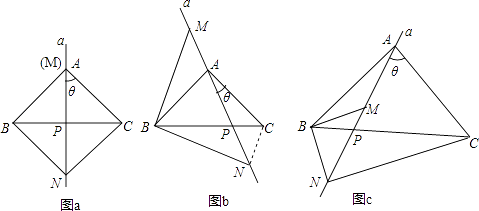
��3����ANC=90�㩁 ![]() ��BAC��
��BAC��
�������£��ߡ�BAC=��MBN��90�㣬AB=AC��BM=BN��
���ABC=��ACB=��BNP= ![]() ��180�㩁��BAC����
��180�㩁��BAC����
�֡ߡ�BPN=��APC��
���BNP�ס�ACP��
�� ![]() =
= ![]() ��
��
�֡ߡ�APB=��CPN��
���ABP�ס�CNP��
���ANC=��ABC��
�ڡ�ABC�У���ABC= ![]() ��180�㩁��BAC��=90�㩁
��180�㩁��BAC��=90�㩁 ![]() ��BAC
��BAC
���������⣺��1���١ߡ�BAC=90�㣬��=45�㣬 ��AP��BC��BP=CP���������������ߺ�һ����
��AP=BP��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룩��
�֡ߡ�MBN=90�㣬BM=BN��
��AP=PN���������������ߺ�һ����
��AP=PN=BP=PC����AN��BC��
���ı���ABNC�������Σ�
���ANC=45�㣻��1����֤���ı���ABNC�������Σ����������εĶԽ���ƽ��һ��Խ�������⣻�ڸ��ݵ���ֱ�������ε����ʿɵá�BNP=��ACB��Ȼ��֤����BNP�͡�ACP���ƣ��������������ζ�Ӧ�߳ɱ����ɵ� ![]() =
= ![]() ���ٸ������߶�Ӧ�ɱ����н���ȿɵá�ABP�͡�CNP���ƣ�Ȼ��������������ζ�Ӧ����ȿɵá�ANC=��ABC���Ӷ��ý⣻��3�����ݵ��������ε�������������BNP=��ACB��Ȼ��֤����BNP�͡�ACP���ƣ��������������ζ�Ӧ�߳ɱ����ɵ�
���ٸ������߶�Ӧ�ɱ����н���ȿɵá�ABP�͡�CNP���ƣ�Ȼ��������������ζ�Ӧ����ȿɵá�ANC=��ABC���Ӷ��ý⣻��3�����ݵ��������ε�������������BNP=��ACB��Ȼ��֤����BNP�͡�ACP���ƣ��������������ζ�Ӧ�߳ɱ����ɵ� ![]() =
= ![]() ���ٸ������߶�Ӧ�ɱ����н���ȿɵá�ABP�͡�CNP���ƣ�Ȼ��������������ζ�Ӧ����ȿɵá�ANC=��ABC��Ȼ����������ε��ڽǺͶ�����ʽ�������ɵý⣮
���ٸ������߶�Ӧ�ɱ����н���ȿɵá�ABP�͡�CNP���ƣ�Ȼ��������������ζ�Ӧ����ȿɵá�ANC=��ABC��Ȼ����������ε��ڽǺͶ�����ʽ�������ɵý⣮