题目内容
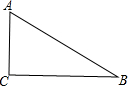
如图,在△ABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB于D,则AD的长度为( )

A.
| B.
| C.
| D.
|

∵在△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=
=
=5(勾股定理).
又∵CD⊥AB于D,
∴
AC•BC=
AB•CD,即3×4=5CD,
解得,CD=
.
故选B.
∴AB=
| BC2+AC2 |
| 42+32 |
又∵CD⊥AB于D,
∴
| 1 |
| 2 |
| 1 |
| 2 |
解得,CD=
| 12 |
| 5 |
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 拼出另一种能证明勾股定理的图形吗?请在图(3)中画出拼后的示意图(无需证明).
拼出另一种能证明勾股定理的图形吗?请在图(3)中画出拼后的示意图(无需证明).
