题目内容
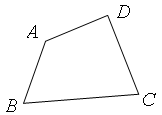
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD、等边△ABE. 已知∠BAC=30º,EF⊥AB,垂足为F,连结DF.

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形。

(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形。
(1)可通过证明△ABC≌△EBF ,得出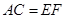
(2)可通过证明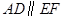 ,且
,且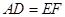 ,从而得出四边形ADFE是平行四边形。
,从而得出四边形ADFE是平行四边形。
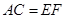
(2)可通过证明
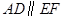 ,且
,且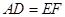 ,从而得出四边形ADFE是平行四边形。
,从而得出四边形ADFE是平行四边形。试题分析:(1)先利用两组角和一组边对应相等,推出两个三角形为全等三角形,再由全等三角形的性质,推出对应边相等。证明:在RT△ABC中,
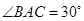 ,
,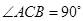 ,所以
,所以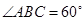 ,而△ABE中,
,而△ABE中,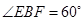 ,
, ,
,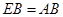 ,所以△ABC≌△EBF ,所以
,所以△ABC≌△EBF ,所以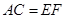
(2)要证明四边形是平行四边形,可以利用一组对边相等且平行来证明。证明:因为△ADC为等边三角形,所以
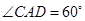 ,又
,又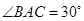 ,所以
,所以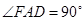 ,又
,又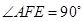 ,所以
,所以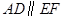 ,又因为△ABC≌△EBF,所以
,又因为△ABC≌△EBF,所以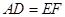 ,所以四边形ADFE是平行四边形。
,所以四边形ADFE是平行四边形。点评:要证明一个四边形是平行四边形,可以利用一组对边平行且相等来证明,也可以用两组对边平行,也可以利用对角线互相平分来证明

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目

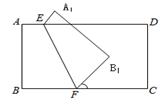

 中,
中, 是
是 边上的一点,
边上的一点,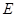 是
是 的中点,过点
的中点,过点 作
作 的延长线于
的延长线于 ,且
,且 ,连接
,连接 .
.
 ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.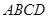 ,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片.如果限定裁剪线最多有两条,能否做到: (用“能”或“不能”填空).若“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.
,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片.如果限定裁剪线最多有两条,能否做到: (用“能”或“不能”填空).若“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.