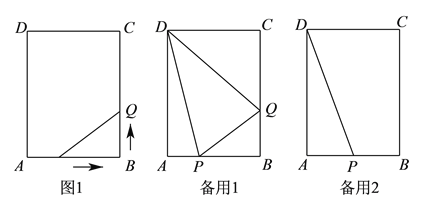
��Ŀ����
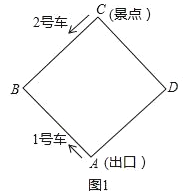
����Ŀ����ͼ��ij�����ڵĻ���·�DZ߳�Ϊ1200��������ABCD������1�š�2�������������ֱ�ӳ���A�;���Cͬʱ������1�ų���A��B��C��D��A·�ߡ�2�ų���C��B��A��D��C·������ѭ����ʻ�����ο���ʱ��ѳ˳����ϡ��³���ʱ����Բ��ƣ��������ٶȾ�Ϊ300��/�֣�
��1����ͼ1������ʻʱ��Ϊt�֣�0��t��8��
��1�ų���2�ų������A��·�̷ֱ�Ϊ_____�ף�_____�ף����ú�t�Ĵ���ʽ��ʾ��
�ڵ���������·����600��ʱ����t��ֵ��
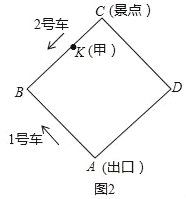
��2����ͼ2���οͼ���BC�ϵ�һ��K�������B��C�غϣ��������˳�������A����CK=x�ף�
���һ�������պô���2�ų��������Ⱥ�˼���������1�ų���
������������պô���1�ų��������Ⱥ�˼���������2�ų���
���ж��οͼ�����������³˳�������A��ʱ�϶ࣿ������ʱ�䣩
���𰸡� 300t 2400��300t
�����������������(1)�ٸ���·��=�ٶ�![]() ʱ����
ʱ����![]() �ij���,���ɵó�����;
�ij���,���ɵó�����;
�ڷ�![]() ��
��![]() ��������ҳ�����
��������ҳ�����![]() ��һԪһ�η���,��֮���ɵó�����;
��һԪһ�η���,��֮���ɵó�����;
(2)��������������οͼ�Ҫ������������ڵľ���,�ٸ���ʱ��=·��![]() �ٶȼ�������οͼ׳˳�������
�ٶȼ�������οͼ׳˳�������![]() ����ʱ��,�ȽϺɵó�����.
����ʱ��,�ȽϺɵó�����.
�����������1���ٵ�![]() ʱ��1�ų������A��·��Ϊ
ʱ��1�ų������A��·��Ϊ![]() �ף�2�ų������A��·��Ϊ
�ף�2�ų������A��·��Ϊ![]() �ף�
�ף�
�ʴ�Ϊ�� ![]() ��
�� ![]()
�ڵ�![]() ʱ����
ʱ����![]()
��ã� ![]()
��![]() ʱ����
ʱ����![]()
��ã� ![]()
��������������������·����600��ʱ�� ![]() ��ֵΪ3��5��
��ֵΪ3��5��
��2���οͼ������һ�³˳�������A��ʱ![]() ���ӣ�
���ӣ�
�οͼ���������³˳�������A��ʱ![]() ���ӣ�
���ӣ�
��![]() ��
��
���οͼ���������³˳�������A��ʱ�϶࣮

����Ŀ��Ϊ����ĸijУ������չУ���γ̽��裬�ƻ���������ѧ���͡�����ѧʵ�顱�������赸���͡��ֹ���֯���ȶ�����ţ�Ҫ��ÿλѧ��������ѡ������һ�����ţ�Ϊ�ˣ���������˱�У���꼶����ѧ��ѡ�����ŵ����������������Ƴ�����ͳ��ͼ��(������)��
ijУ������ѧ��ѡ����������ͳ�Ʊ�
ѡ������ | ��ѧ���� | ��ѧʵ�� | �����赸 | �ֹ���֯ | ���� |
��ռ�ٷֱ� | a | 35% | b | 10% | c |

����ͳ��ͼ���е���Ϣ������������⣺
(1)�ε����ѧ����������a��b��c��ֵ��
(2)������ͳ��ͼ����������