题目内容
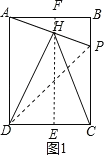
【题目】如图,已知矩形ABCD,P为BC上的一点,连接AP,过D点作DH⊥AP于H,AB=![]() , BC=4,当△CDH为等腰三角形时,则BP=_________________.
, BC=4,当△CDH为等腰三角形时,则BP=_________________.

【答案】![]() 、
、![]() 或2
或2
【解析】
分HD=HC、DH=DC以及CH=CD三种情况考虑:
①当HD=HC时,过点H作HE⊥CD于点E,延长EH交AB于点F,连接DP,由△CDH为等腰三角形得出点H为AP的中点,再结合DH⊥AP可得出AD=DP,设BP=a,利用勾股定理即可得出关于a的一元二次方程,解方程即可得出结论;
②当DH=DC时,利用勾股定理可求出AH的长度,进而得出∠DAH=45°,由平行线的性质可得出∠APB=45°,进而得出△ABP为等腰直角三角形,即BP=AB;
③当CH=CD时,过点C作CE⊥DH于点E,延长CE交AD于点F,根据等腰三角形的性质即可得出DF=AF![]() AD,由DH⊥CF、DH⊥AP即可得出CF∥AP,结合AF∥CP即可得出四边形AFCP为平行四边形,进而得出AF=CP,再根据平行线的性质即可得出AF的长度,结合BC的长度以及AF=CP即可求出BP的长度.
AD,由DH⊥CF、DH⊥AP即可得出CF∥AP,结合AF∥CP即可得出四边形AFCP为平行四边形,进而得出AF=CP,再根据平行线的性质即可得出AF的长度,结合BC的长度以及AF=CP即可求出BP的长度.
①当HD=HC时,过点H作HE⊥CD于点E,延长EH交AB于点F,连接DP,如图1所示.
∵HD=HC,∴点E为CD的中点.
∵EF∥AD,∴FH为△ABP的中位线,∴AH=HP.
∵DH⊥AP,∴△DAP为等腰三角形,∴AD=DP.
设BP=a,则CP=4﹣a,由勾股定理得:DP2=CD2+CP2,即16=8+(4﹣a)2,解得:a=4﹣2![]() ,或a=﹣4﹣2
,或a=﹣4﹣2![]() (舍去);
(舍去);
②当DH=DC时,如图2所示.
∵DC=AB=2![]() ,∴DH=2
,∴DH=2![]() .
.
在Rt△AHD中,AD=4,DH=2![]() ,∴AH
,∴AH![]() 2
2![]() ,∴AH=DH,∴∠DAH=∠ADH=45°.
,∴AH=DH,∴∠DAH=∠ADH=45°.
∵AD∥BC,∴∠APB=∠DAH=45°.
∵∠B=90°,∴△ABP为等腰直角三角形,∴BP=AB=2![]() ;
;
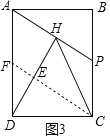
③当CH=CD时,过点C作CE⊥DH于点E,延长CE交AD于点F,如图3所示.
∵CH=CD,CE⊥DH,∴DE=HE![]() DH.
DH.
∵DH⊥CF,DH⊥AP,∴CF∥AP.
∵AF∥CP,∴四边形AFCP为平行四边形,∴AF=CP.
∵EF∥AH,DE=HE,∴DF=AF![]() AD=2,∴BP=BC﹣CP=BC﹣AF=4﹣2=2.
AD=2,∴BP=BC﹣CP=BC﹣AF=4﹣2=2.
综上所述:BP的长度为![]() 、
、![]() 或2.
或2.
故答案为:![]() 、
、![]() 或2.
或2.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案