题目内容
某种商品的进价为每件50元,售价为每件60元.为了促销,决定凡是购买10件以上的,每多买一件,售价就降低0.10元(例如,某人买20件,于是每件降价0.10×(20-10)=1元,就可以按59元/件的价格购买),但是最低价为55元/件.同时,商店在出售中,还需支出税收等其他杂费1.6元/件.
(1)求顾客一次至少买多少件,才能以最低价购买?
(2)写出当出售x件时(x>10),利润y(元)与出售量x(件)之间的函数关系式;
(3)有一天,一位顾客买了47件,另一位顾客买了60件,结果发现卖了60件反而比卖了47件赚的钱少.为了使每次卖的越多赚的钱也越多,在其他促销条件不变的情况下,最低价55元/件至少要提高到多少?为什么?
(1)求顾客一次至少买多少件,才能以最低价购买?
(2)写出当出售x件时(x>10),利润y(元)与出售量x(件)之间的函数关系式;
(3)有一天,一位顾客买了47件,另一位顾客买了60件,结果发现卖了60件反而比卖了47件赚的钱少.为了使每次卖的越多赚的钱也越多,在其他促销条件不变的情况下,最低价55元/件至少要提高到多少?为什么?
(1)60;(2)当10<x≤60时,y=-0.1x2+9.4x;当x>60时,y=3.4x;(3)56.3元
试题分析:(1)设顾客一次至少购买x件,根据“购买10件以上的,每多买一件,售价就降低0.10元”即可列方程求解;
(2)分当10<x≤60时,当x>60时,这两种情况,根据“购买10件以上的,每多买一件,售价就降低0.10元”即可列出函数关系式;
(3)先把(2)中当10<x≤60时,对应的函数关系式配方,再根据二次函数的性质求解即可.
(1)设顾客一次至少购买x件,由题意得
60-0.1(x-10)=55,解得x=60
答:顾客一次至少买60件,才能以最低价购买;
(2)当10<x≤60时,y=[60-0.1(x-10)-50]x-1.6x=-0.1x2+9.4x
当x>60时,y=(55-50-1.6)x=3.4x;
(3)利润y=-0.1x2+9.4x=-0.1(x-47)2+220.9,
∵当x=47时,利润y有最大值,而超过47时,利润y反而减少.
要想卖的越多赚的越多,即
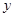 随
随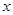 的增大而增大,
的增大而增大,由二次函数性质可知,x≤47,
∴当x=47时,最低售价应定为60-0.1×(47-10)=56.3元.
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
相关题目
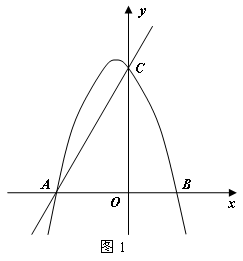
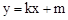 与x轴、y轴分别交于A、C两点,抛物线
与x轴、y轴分别交于A、C两点,抛物线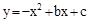 经过A、C两点,点B是抛物线与x轴的另一个交点,当
经过A、C两点,点B是抛物线与x轴的另一个交点,当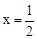 时,y取最大值
时,y取最大值 .
.
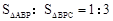 ,求点P的坐标;
,求点P的坐标; 与(1)中所求的抛物线交于M、N两点,问:
与(1)中所求的抛物线交于M、N两点,问: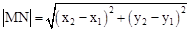 )
) 米。(1)若垂直于墙的一边长为
米。(1)若垂直于墙的一边长为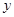 米,直接写出
米,直接写出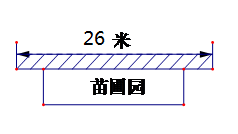

 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=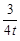 x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
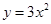 向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
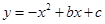 的部分图象如图所示,若
的部分图象如图所示,若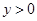 ,则x的取值范围是( )
,则x的取值范围是( )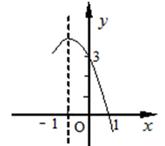
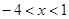
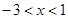
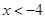 或
或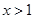
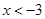 或
或