题目内容
已知抛物线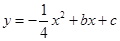 与
与 轴交于
轴交于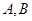 两点,与
两点,与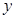 轴交于点
轴交于点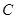 ,连结
,连结 ,
, 是线段
是线段 上一动点,以
上一动点,以 为一边向右侧作正方形
为一边向右侧作正方形 ,连结
,连结 .若
.若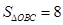 ,
, .
.

(1)求抛物线的解析式;
(2)求证: ;
;
(3)求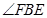 的度数;
的度数;
(4)当 点沿
点沿 轴正方向移动到点
轴正方向移动到点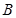 时,点
时,点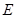 也随着运动,则点
也随着运动,则点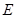 所走过的路线长是 .
所走过的路线长是 .
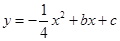 与
与 轴交于
轴交于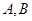 两点,与
两点,与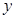 轴交于点
轴交于点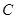 ,连结
,连结 ,
, 是线段
是线段 上一动点,以
上一动点,以 为一边向右侧作正方形
为一边向右侧作正方形 ,连结
,连结 .若
.若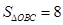 ,
, .
.
(1)求抛物线的解析式;
(2)求证:
 ;
;(3)求
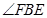 的度数;
的度数;(4)当
 点沿
点沿 轴正方向移动到点
轴正方向移动到点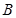 时,点
时,点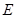 也随着运动,则点
也随着运动,则点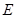 所走过的路线长是 .
所走过的路线长是 .(1) ;(2)由(1)得点B、C的坐标,即可得到
;(2)由(1)得点B、C的坐标,即可得到 ,证得
,证得 ≌
≌ ,根据全等三角形的性质求解即可;(3)45°;(4)
,根据全等三角形的性质求解即可;(3)45°;(4)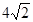
 ;(2)由(1)得点B、C的坐标,即可得到
;(2)由(1)得点B、C的坐标,即可得到 ,证得
,证得 ≌
≌ ,根据全等三角形的性质求解即可;(3)45°;(4)
,根据全等三角形的性质求解即可;(3)45°;(4)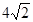
试题分析:(1)由
 可知此抛物线的对称轴是
可知此抛物线的对称轴是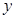 轴,即
轴,即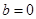 ,即可求得点B、C的坐标,再根据三角形的面积公式求解即可;
,即可求得点B、C的坐标,再根据三角形的面积公式求解即可;(2)由(1)得点B、C的坐标,即可得到
 ,证得
,证得 ≌
≌ ,根据全等三角形的性质求解即可;
,根据全等三角形的性质求解即可;(3)作
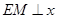 轴,交
轴,交 于点
于点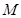 ,易证
,易证 ≌
≌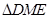 ,所以
,所以 ,
,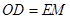 ,又因为
,又因为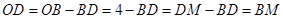 ,即得
,即得 ,从而可以求得结果;
,从而可以求得结果;(4)由(3)知,点
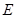 在定直线上,当
在定直线上,当 点沿
点沿 轴正方向移动到点
轴正方向移动到点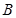 时,即得点
时,即得点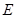 所走过的路线长.
所走过的路线长.(1)由
 ,可知此抛物线的对称轴是
,可知此抛物线的对称轴是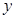 轴,即
轴,即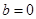
所以

由
 ,得
,得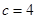
抛物线解析式为
 ;
;(2)由(1)得
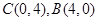
所以

在
 和
和 中
中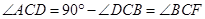 ,
,
所以
 ≌
≌
所以

所以
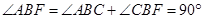
所以
 ;
;(3)作
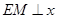 轴,交
轴,交 于点
于点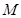
易证
 ≌
≌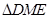
所以
 ,
,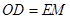
又因为

所以

因为

所以
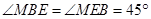 ;
;(4)由(3)知,点
 在定直线上
在定直线上当
 点沿
点沿 轴正方向移动到点
轴正方向移动到点 时,
时,点
 所走过的路线长等于
所走过的路线长等于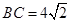 .
.点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
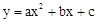 (a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
 (a、m为常数,且a¹0)。
(a、m为常数,且a¹0)。 中,其函数
中,其函数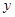 与自变量
与自变量 之间的部分对应值如下表所示:
之间的部分对应值如下表所示: ,
, )、B(
)、B(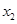 ,
,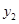 )在该函数的图象上,则当
)在该函数的图象上,则当
 时,
时, 米。(1)若垂直于墙的一边长为
米。(1)若垂直于墙的一边长为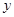 米,直接写出
米,直接写出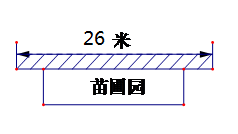
 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为(-1,0),过点C的直线y=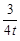 x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
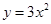 向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 .
向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为 . 的图象如图所示,则一次函数
的图象如图所示,则一次函数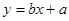 的图象不经过( ).
的图象不经过( ).