题目内容
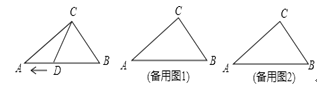
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.
(1)如图1,直接写出∠ABD的大小(用含α的式子表示);
(2)如图2,若∠BCE=150°,∠ABE=60°, ∠DEC=45°,求α的值;
(3)如图3,若∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明.

【答案】(1)30-![]() α;(2)α=30°(3)△ABE是等边三角形,理由见解析.
α;(2)α=30°(3)△ABE是等边三角形,理由见解析.
【解析】
(1)根据等腰三角形的性质求出∠ABC的度数,即可求出答案;
(2)连接AD,CD,由旋转的性质可证△BCD为等边三角形,根据SSS证明△ABD≌△ACD,可得∠BAD=∠CAD,∠ADB=∠ADC;根据AAS证明△ABD≌△EBC(AAS),可得∠EBC=∠ABD=30-![]() α;然后再证明△DEC为等腰直角三角形,得到DC=CE=BC,根据∠EBC=30-
α;然后再证明△DEC为等腰直角三角形,得到DC=CE=BC,根据∠EBC=30-![]() α=15可求出α的值;
α=15可求出α的值;
(3)由△ABD≌△EBC和∠ABE=60°,可证△ABE是等边三角形.
解:(1)∵AB=AC,∠A=α,
∴∠ABC=∠ACB=![]() (180-∠A)=90-
(180-∠A)=90-![]() α,
α,
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,
∴∠ABD=30-![]() α,
α,
故答案为30-![]() α;
α;
(2)如图2,连接AD,CD,
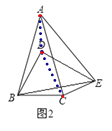
∵线段BC绕B逆时针旋转60°得到线段BD,
则BC=BD,∠DBC=60°,
∵∠ABE=60°,
∴∠ABD=60°-∠DBE=∠EBC=30°-![]() α,且△BCD为等边三角形,
α,且△BCD为等边三角形,
∴BD=CD,∠BDC=60°.
在△ABD与△ACD中,
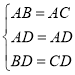 ,
,
∴△ABD≌△ACD,
∴∠BAD=∠CAD,∠ADB=∠ADC,
∵∠BDC=60°,
∴∠ADB=∠ADC=150°,
∴∠ADB=∠BCE.
∵∠ABD=60°-DBE, ∠CBE=60°-∠DBE,
∴∠ABD=∠EBC.
在△ABD和△EBC中
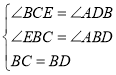 ,
,
∴△ABD≌△EBC(AAS),
∴∠EBC=∠ABD=30-![]() α.
α.
∵∠BCD=60°,∠BCE=150°,
∴∠DCE=150°-60°=90°,
∵∠DEC=45°,
∴△DEC为等腰直角三角形,
∴DC=CE=BC,
∵∠BCE=150°,
∴∠EBC=![]() (180°-150°)=15°,
(180°-150°)=15°,
∵∠EBC=30-![]() α=15,
α=15,
∴α=30°.
(3)△ABE是等边三角形,
由(2)知△ABD≌△EBC
∴AB=BE,
∵∠ABE=60°,
∴△ABE是等边三角形;